尺度不变特征变换SIFT
Published in：2023-07-11 | category： Computer Technology
Words: 6k | Reading time: 21min | reading：

SIFT

尺度不变特征变换（Scale-Invariant Feature Transform，SIFT）是一种用于计算机视觉和图像处理的算法。它是由David Lowe在1999年提出的，并成为一种广泛应用的特征提取和匹配方法。

SIFT算法的主要目标是从图像中提取出具有尺度不变性的特征点，并能够在不同尺度、旋转和亮度条件下进行匹配。它在计算机视觉领域被广泛用于图像识别、目标检测和图像拼接等任务。

SIFT算法的主要步骤包括：

  1. 尺度空间极值检测：通过构建高斯金字塔，检测图像在不同尺度上的局部极值点，这些点往往对应于具有不同尺度的特征。

  2. 关键点定位：在尺度空间的极值点上，通过利用图像的梯度信息和曲率来选择稳定的关键点。这些关键点通常位于图像中的角点、边缘等显著的位置。

  3. 方向分配：为每个关键点分配一个主导方向，使得特征具有旋转不变性。这通常通过计算关键点周围区域的梯度方向直方图来实现。

  4. 特征描述：在关键点附近的局部区域内，构建描述子，用来表示关键点周围的图像特征。描述子通常基于局部图像梯度的方向和强度信息，具有尺度和旋转不变性。

  5. 特征匹配：通过比较不同图像的特征描述子，利用特征间的相似度进行匹配。常用的方法是计算特征向量之间的欧氏距离或相似性度量，选择最佳的匹配对。

SIFT算法的关键在于其对尺度和旋转的不变性，使得它能够在不同视角和条件下进行可靠的特征匹配。这使得SIFT成为许多计算机视觉应用中的重要工具。

尺度空间极值检测

尺度空间极值检测（Scale-space extrema detection）是一种在不同尺度上检测图像中的极值点的方法，用于寻找具有尺度不变性的特征点。该方法通常与尺度不变特征变换（SIFT）算法相关联。

尺度空间极值检测的基本思想是通过在图像的不同尺度上应用高斯滤波器，来寻找在不同尺度上的局部极值点。具体步骤如下：

  1. 构建尺度空间金字塔：从原始图像开始，应用一系列的高斯滤波器，每个滤波器具有不同的尺度参数（标准差），生成一组具有不同模糊程度的图像。这些图像构成了尺度空间金字塔，其中较高层次的图像尺度比较小，具有更高的模糊程度。

  2. 在尺度空间的每一层上，比较每个像素的值与其邻域像素的值，找到局部极值点。极值点是指在一个局部邻域内，像素的值在该邻域中最大或最小。

  3. 对于找到的极值点，根据其响应值（如像素值或梯度大小）进行阈值处理和边界消除。通常，会设置一个阈值来筛选出具有较大响应值的极值点，同时通过非极大值抑制（non-maximum suppression）来消除邻域内的重复极值点。

通过尺度空间极值检测，可以在不同尺度上发现具有尺度不变性的特征点，例如角点、边缘和斑点等。这些特征点可以在不同的尺度、旋转和光照条件下保持稳定，成为计算机视觉中许多任务（如目标检测、图像匹配和三维重建）的重要基础。

构建尺度空间金字塔

构建尺度空间金字塔（Scale Space Pyramid）是指通过一系列图像处理操作，在不同尺度上构建一组具有不同模糊程度的图像集合，用于分析和处理图像。

构建尺度空间金字塔的一般步骤如下：

  1. 初始层：将原始图像作为尺度空间金字塔的第一层。这是金字塔的最底层，也是原始图像的未经处理的版本。

  2. 下采样：对当前层次的图像进行下采样（如降采样），即减小图像的尺寸。下采样可以通过丢弃一些像素或使用插值等方法实现。这样可以生成一个比原始图像尺寸更小的图像。

  3. 高斯滤波：对下采样后的图像应用高斯滤波器。高斯滤波器通过在图像上进行卷积操作，对图像进行平滑处理。高斯滤波器的模糊程度由标准差参数决定。

  4. 重复步骤2和步骤3：依次对每个层次的图像进行下采样和高斯滤波的操作，直到达到所需的尺度或图像大小。

通过重复执行下采样和高斯滤波操作，我们可以在不同尺度上构建一系列图像，形成尺度空间金字塔。每个层次的图像都对应于原始图像在不同尺度上的模糊版本。较高层次的图像具有更小的尺度和更高的模糊程度。

构建尺度空间金字塔的目的是为了在不同尺度上分析和处理图像，以提取尺度不变的特征，并在不同尺度上实现鲁棒的图像处理操作。尺度空间金字塔在计算机视觉领域的许多任务中都具有重要的应用，例如特征检测、目标识别和图像金字塔等。

示例 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import cv2
import os


def generate_scale_space_pyramid(image, num_octaves, num_scales):
    pyramid = []

    # 生成图像金字塔的初始层
    pyramid.append(image)

    # 设置每个八度的尺度数量
    scales_per_octave = num_scales - 1

    for octave in range(num_octaves):
        octave_images = []

        # 获取当前八度的第一张图像
        base_image = pyramid[octave * scales_per_octave]

        # 生成当前八度的尺度空间
        for scale in range(1, num_scales):
            sigma = 2 ** (octave + (scale / scales_per_octave))  # 计算当前尺度的标准差
            scaled_image = cv2.GaussianBlur(base_image, (0, 0), sigmaX=sigma, sigmaY=sigma)
            octave_images.append(scaled_image)

        # 将当前八度的图像加入到金字塔中
        pyramid.extend(octave_images)

        # 缩小基础图像作为下一个八度的起始图像
        base_image = cv2.resize(base_image, (0, 0), fx=0.5, fy=0.5)
        pyramid.append(base_image)

    return pyramid
示例

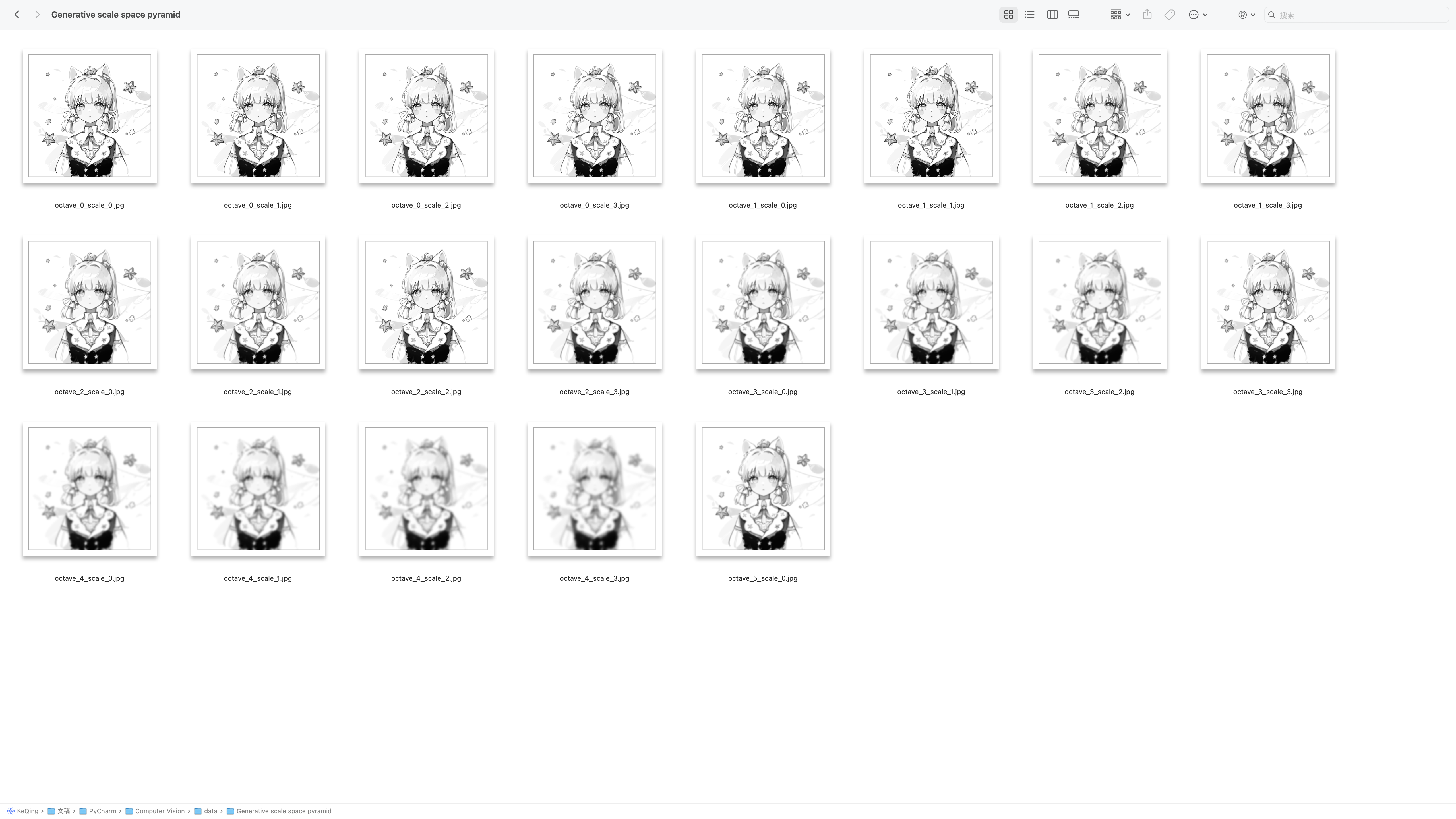
在尺度空间金字塔中，”octave”（八度）和 “scale”（尺度）是用来描述金字塔的层级结构和尺度级别的参数。

  • 八度（octave）：尺度空间金字塔按照一种对数尺度进行组织，每个八度对应着一个特定的尺度范围。每个八度中，金字塔的每一层图像都是在基础图像上进行下采样得到的。八度的数量决定了金字塔的层级结构和尺度的覆盖范围。
  • 尺度（scale）：每个八度中，金字塔的每一层都对应着一个特定的尺度级别。尺度是通过应用不同程度的高斯滤波器来实现的，而高斯滤波器的标准差（sigma）用于控制图像的模糊程度。每个尺度级别的图像都是基于前一个尺度级别的图像进行高斯模糊得到的。

在尺度空间金字塔中，八度和尺度共同确定了金字塔的层级结构和图像的模糊程度。不同的八度和尺度组合产生不同程度的图像模糊，并在尺度上覆盖了不同的细节和结构。

在代码示例中，octave 表示当前图像所在的八度，scale 表示当前图像所在的尺度。这些参数用于生成尺度空间金字塔，并在保存图像时作为命名的一部分，以方便识别图像所属的八度和尺度级别。

八度（Octave）尺度（Scale）图像文件名
00octave_0_scale_0.jpg
01octave_0_scale_1.jpg
02octave_0_scale_2.jpg
03octave_0_scale_3.jpg
10octave_1_scale_0.jpg
11octave_1_scale_1.jpg
12octave_1_scale_2.jpg
13octave_1_scale_3.jpg
20octave_2_scale_0.jpg
21octave_2_scale_1.jpg
22octave_2_scale_2.jpg
23octave_2_scale_3.jpg
30octave_3_scale_0.jpg
31octave_3_scale_1.jpg
32octave_3_scale_2.jpg
33octave_3_scale_3.jpg
40octave_4_scale_0.jpg
41octave_4_scale_1.jpg
42octave_4_scale_2.jpg
43octave_4_scale_3.jpg
50octave_5_scale_0.jpg

图像尺度空间

图像尺度空间（Scale Space）是在不同尺度上对图像进行模糊处理，以便在不同尺度上分析和检测图像中的特征和结构。尺度空间理论在计算机视觉和图像处理中起着重要的作用，它允许我们在不同的尺度上对图像进行分析，并提取出尺度不变的特征。

在尺度空间中，通过应用一系列不同程度的高斯滤波器对图像进行模糊处理，从而得到一组具有不同模糊程度的图像。每个模糊图像表示了原始图像在不同尺度上的平滑版本。高斯滤波器的尺度参数决定了图像的模糊程度，较小的尺度对应于较细的细节，较大的尺度对应于较粗的结构。

图像尺度空间的构建可以通过以下步骤实现：

  1. 选择一个初始尺度空间：在初始尺度上对图像应用高斯滤波器，得到第一层模糊图像。

  2. 生成尺度空间金字塔：对初始尺度图像进行下采样（如降采样），并在每个下采样层次上应用高斯滤波器，得到一组不同尺度的模糊图像。这形成了一个尺度空间金字塔，其中较高层次的图像尺度比较小，具有更高的模糊程度。

  3. 图像插值：由于下采样会导致图像信息的丢失，为了在不同尺度之间进行精确的插值，可以使用插值技术（如双线性插值）来恢复图像的分辨率。

通过构建尺度空间，我们可以在不同尺度上检测和分析图像中的特征，例如边缘、角点和斑点等。这种尺度不变性对于许多计算机视觉任务（如目标检测、特征匹配和图像拼接）非常重要，因为它允许我们在不同的尺度上对图像进行鲁棒的处理和分析。

高斯滤波器

高斯滤波器（Gaussian filter）是一种常用的线性平滑滤波器，用于对图像进行平滑处理和去除噪声。它基于高斯函数的数学模型，通过对图像进行卷积运算来实现。

高斯函数是一种钟形曲线，具有以下的形式：

$G(x, y) = \frac{1}{2\pi\sigma^2} \cdot e^{-\frac{x^2 + y^2}{2\sigma^2}}$

其中，G(x, y)是高斯函数的值，x和y是平面上的坐标，σ是高斯函数的标准差。高斯函数的标准差决定了函数的形状和宽度，较大的标准差会导致更宽的函数曲线。

在图像处理中，高斯滤波器将高斯函数应用于图像的每个像素点，并以该像素点为中心计算一个加权平均值。这个加权平均值是通过对滤波器内的邻域像素进行加权平均来计算的，权重由高斯函数确定，距离中心像素越远的像素具有更小的权重。

通过对图像应用高斯滤波器，可以实现以下效果：

  1. 平滑图像：高斯滤波器可以模糊图像，减少图像中的噪声和细节，从而得到一个平滑的版本。

  2. 去除噪声：由于高斯滤波器对噪声具有平滑作用，它可以在图像中降低噪声的影响，提高图像的质量。

  3. 缩小细节：较大的高斯滤波器会导致图像的细节被模糊，从而可以用于图像的降采样和特征提取。

选择适当的高斯滤波器的标准差是很重要的，它决定了滤波器的模糊程度。较小的标准差对应于较细的模糊效果，较大的标准差对应于较强的模糊效果。通常根据应用的需求和图像的特点来选择合适的标准差。

示例 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import cv2
import numpy as np

def apply_gaussian_blur(image_path, kernel_size, sigma, output_path):
    # 读取图像
    image = cv2.imread(image_path)

    # 将图像转换为灰度图
    gray_image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)

    # 应用高斯滤波器
    blurred_image = cv2.GaussianBlur(gray_image, kernel_size, sigma)

    # 保存滤波后的图像
    cv2.imwrite(output_path, blurred_image)
kernel_size345
sigma原图
1.0kernel_size=3&sigma=1.0kernel_size=45&sigma=1.0
2.0kernel_size=45&sigma=2.0kernel_size=45&sigma=2.0
3.0kernel_size=45&sigma=3.0kernel_size=45&sigma=3.0

高斯函数（Gaussian function）是一种常见的数学函数，它以德国数学家卡尔·弗里德里希·高斯（Carl Friedrich Gauss）命名，具有以下的数学表达式：
$G(x) = \frac{1}{\sqrt{2\pi\sigma^2}} \cdot e^{-\frac{x^2}{2\sigma^2}}$
其中，( G(x) ) 是高斯函数的值，( x ) 是自变量，( \sigma ) 是标准差（standard deviation）。
高斯函数的图像呈现出典型的钟形曲线形状，其峰值位于均值（mean）处，曲线两侧逐渐衰减。标准差决定了曲线的宽度，较大的标准差会使曲线更宽，较小的标准差会使曲线更尖锐。
高斯函数在许多领域中具有重要的应用，尤其在统计学和信号处理中。它具有许多优良的数学性质，例如：

  • 高斯函数是连续函数，定义域为负无穷到正无穷的实数集。
  • 高斯函数在整个实轴上的积分为1，即满足归一性。
  • 高斯函数是平移不变的，即对于任何常数 ( a )，当自变量 ( x ) 替换为 ( x-a ) 时，函数值保持不变。

高斯函数在图像处理和模式识别中也经常被用作滤波器的基础，通过在空域或频域上应用高斯函数，可以实现图像平滑、噪声抑制和特征提取等操作。

找到局部极值点

构建高斯差分金字塔

在尺度空间的每一层上，比较每个像素的值与其邻域像素的值，是一种常见的操作用于寻找局部极值点。极值点是指在一个局部邻域内，像素的值在该邻域中最大或最小。

具体步骤如下：

  1. 对于尺度空间金字塔的每一层图像，遍历每个像素。

  2. 对于每个像素，将其与其相邻像素进行比较。通常采用3x3或5x5大小的邻域。

  3. 如果像素的值在邻域内是最大或最小的，那么它被认为是一个局部极值点。

通过比较像素与其邻域像素的值，可以确定局部极值点，即在一个局部邻域内像素值最大或最小的点。这些极值点具有一定的稳定性和重要性，常用于计算机视觉中的特征提取和特征匹配任务。

在尺度不变特征变换（SIFT）算法中，这一步是尺度空间极值检测的关键步骤。通过在不同尺度上比较像素与邻域像素的值，可以找到具有尺度不变性的特征点，这些特征点对于图像匹配、目标识别等任务非常有用。

DoG（Difference of Gaussians）是通过计算尺度空间金字塔中相邻层级之间的差分得到的一种图像增强技术。它可以用于边缘检测、纹理分析等计算机视觉任务。
DoG的定义公式为：
$$\text{DoG}(x, y, \sigma) = G(x, y, k\sigma) - G(x, y, \sigma)$$
其中，$(x, y)$ 是图像中的像素坐标，$\sigma$ 是高斯滤波器的标准差，$k$ 是尺度因子（通常为较大的值，例如 $k = 1.6$），$G(x, y, \sigma)$ 是高斯滤波器函数。
通过将不同尺度空间金字塔层级的高斯滤波结果相减，DoG可以突出图像中的边缘和纹理信息。边缘和纹理通常在不同尺度上具有不同的空间特征尺度，因此通过计算不同尺度层级之间的差分，可以增强这些特征并提取出来。
在实际应用中，DoG通常用于图像金字塔的构建和尺度空间极值点检测，是一种常用的特征提取方法之一。

精确定位极值点

使用泰勒级数展开的目的是为了精确定位尺度空间金字塔中的极值点，即找到极值点的精确位置和尺度。

在尺度空间金字塔中，极值点通常是通过比较每个像素的值与其邻域像素的值来找到的。然而，通过简单比较像素值可能只能得到粗略的位置估计，并不能精确定位极值点。

为了更精确地定位极值点，可以使用泰勒级数展开来近似极值点的位置和尺度。泰勒级数展开是一种将函数在某个点处进行多项式逼近的方法。

对于极值点的位置 $(x, y)$，我们可以使用二维泰勒级数展开来近似其精确位置：

$$f(x + \Delta x, y + \Delta y) \approx f(x, y) + \frac{\partial f}{\partial x}\Delta x + \frac{\partial f}{\partial y}\Delta y + \frac{1}{2}\left(\frac{\partial^2 f}{\partial x^2}\Delta x^2 + \frac{\partial^2 f}{\partial y^2}\Delta y^2\right)$$

其中，$\Delta x$ 和 $\Delta y$ 是相对于极值点位置 $(x, y)$ 的偏移量。通过对函数 $f(x, y)$ 进行一阶和二阶偏导数计算，我们可以获得这些导数值。通过求解泰勒级数展开的偏导数为零的方程组，可以解得 $\Delta x$ 和 $\Delta y$，从而得到更精确的极值点位置。

对于极值点的尺度，我们可以使用一维泰勒级数展开来近似其精确尺度：

$$f(x, y, \sigma + \Delta\sigma) \approx f(x, y, \sigma) + \frac{\partial f}{\partial \sigma}\Delta\sigma + \frac{1}{2}\frac{\partial^2 f}{\partial \sigma^2}\Delta\sigma^2$$

其中，$\Delta\sigma$ 是相对于极值点尺度 $\sigma$ 的偏移量。通过对函数 $f(x, y, \sigma)$ 进行一阶和二阶偏导数计算，我们可以获得这些导数值。通过求解泰勒级数展开的偏导数为零的方程，可以解得 $\Delta\sigma$，从而得到更精确的极值点尺度。

通过使用泰勒级数展开，我们可以对极值点的位置和尺度进行更精确的估计，从而实现对尺度空间金字塔中极值点的精确定位。

阈值处理和边界消除

阈值处理和边界消除是在找到尺度空间金字塔中的极值点后对这些极值点进行进一步处理的步骤。

阈值处理是通过设置一个阈值来筛选具有较大响应值的极值点。阈值可以根据任务需求进行设定，通常选择一个合适的响应值阈值，以保留具有足够显著特征的极值点，而剔除那些响应值较低的不太重要的极值点。

边界消除是为了消除在邻域内出现的重复极值点。在尺度空间金字塔中，由于不同尺度层级之间的重叠区域，可能存在邻域内的极值点重复出现的情况。为了保留唯一的极值点，需要应用边界消除技术，通常使用非极大值抑制（non-maximum suppression）来实现。

非极大值抑制是一种常用的边界消除方法，用于消除邻域内的重复极值点。对于每个局部极值点，非极大值抑制会比较其响应值与邻域内的其他点的响应值，并保留具有最大响应值的极值点，而抑制其他点。这样可以确保在同一局部区域内只保留一个最显著的极值点。

阈值处理和边界消除是在极值点检测后对极值点进行筛选和优化的重要步骤。它们可以帮助我们提取出具有足够显著特征的稳定极值点，用于后续的计算机视觉任务，如特征提取、特征匹配等。

阈值处理

阈值处理是一种简单的图像处理操作，用于将图像中的像素值与设定的阈值进行比较，并根据比较结果对像素进行分类或处理。

以下是一种基本的阈值处理方法：

  1. 确定阈值：首先需要确定阈值的数值，可以根据具体应用场景和需求进行设定。阈值可以是一个固定值，也可以根据图像的特性和统计信息进行自适应调整。

  2. 进行比较：将图像中的每个像素与阈值进行比较。通常，如果像素值大于阈值，则被归类为一类（例如，被认为是前景像素）；如果像素值小于阈值，则被归类为另一类（例如，被认为是背景像素）。

  3. 分类或处理：根据比较的结果，对图像像素进行分类或处理。可以根据实际需求将像素分为不同的类别，如二值图像（只有两个像素值，通常是0和255）、灰度图像（多个像素值，表示不同的灰度级别）或进行其他特定的处理操作，如目标检测、边缘提取等。

在具体实现阈值处理时，可以使用图像处理库或工具来简化操作。例如，在Python中，可以使用OpenCV库的函数cv2.threshold()来实现阈值处理。该函数接受输入图像和设定的阈值，并返回处理后的图像。

阈值处理是图像处理中的基础操作，常用于图像分割、二值化、目标检测等应用中。根据具体的应用需求，可以根据不同的阈值处理方法和策略来实现所需的图像处理效果。

消除边界响应

Hessian矩阵

Hessian矩阵是一个二阶偏导数矩阵，用于描述多元函数的局部曲率和形状信息。它由函数的所有二阶偏导数构成的方阵。

对于一个具有多个自变量的函数，Hessian矩阵的元素表示该函数在不同自变量方向上的曲率。具体而言，Hessian矩阵的第 $(i, j)$ 元素表示函数关于第 $i$ 个自变量和第 $j$ 个自变量的二阶偏导数。

Hessian矩阵可以用来分析函数的驻点（即梯度为零的点）和极值点。根据Hessian矩阵的特征值和特征向量，可以判断一个驻点的类型，例如判断其是否为极大值、极小值或鞍点。具体而言，如果Hessian矩阵的所有特征值均为正，则该点为极小值；如果所有特征值均为负，则为极大值；如果特征值既有正又有负，则为鞍点。

在计算机视觉和图像处理领域，Hessian矩阵常用于特征检测和图像处理算法中。例如，在尺度不变特征变换（SIFT）算法中，通过计算图像中的Hessian矩阵的特征值和特征向量，可以检测出具有稳定尺度和方向的关键点。Hessian矩阵的分析可以帮助提取图像中的关键特征，并用于特征匹配和目标识别等任务。

$$
\text{Hessian}(f) =
\begin{bmatrix}
\frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1 \partial x_2} & \ldots & \frac{\partial^2 f}{\partial x_1 \partial x_n} \
\frac{\partial^2 f}{\partial x_2 \partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \ldots & \frac{\partial^2 f}{\partial x_2 \partial x_n} \
\vdots & \vdots & \ddots & \vdots \
\frac{\partial^2 f}{\partial x_n \partial x_1} & \frac{\partial^2 f}{\partial x_n \partial x_2} & \ldots & \frac{\partial^2 f}{\partial x_n^2}
\end{bmatrix}
$$

其中，$\frac{\partial^2 f}{\partial x_i \partial x_j}$ 表示函数 $f$ 对第 $i$ 个自变量和第 $j$ 个自变量的二阶偏导数。

CV
Prev:
7.13-7.16技术培训实记
Next:
我的树

    • Copyright © 2023 - 2024 kclx | Powered by Hexo | Theme Bamboo