matplotlib简析
Published in：2023-07-27 | category： Computer Technology
Words: 22.1k | Reading time: 92min | reading：

matplotlib简析

Matplotlib是一个用于创建静态、动态和交互式图表的Python绘图库。它提供了广泛的功能，使用户能够可视化数据和结果，从简单的线条图和散点图到复杂的图形，如条形图、直方图、饼图、3D图形等。

Matplotlib是Python数据科学生态系统中最流行的绘图库之一，它支持几乎所有操作系统，并且可以与多个图形工具包和界面结合使用，如NumPy、Pandas、SciPy等。此外，Matplotlib还可以嵌入到图形用户界面（GUI）工具包中，如Tkinter、PyQt等，从而实现交互式图形应用程序的开发。

Matplotlib的主要优势包括易于使用、灵活性和功能强大。使用Matplotlib，您可以以高质量和专业的方式展示数据，这对于数据分析、科学研究、工程和其他领域都是非常有用的。

Matplotlib官网

https://matplotlib.org/

绘图类型

绘图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import matplotlib.pyplot as plt
import numpy as np

plt.style.use('_mpl-gallery')

# make data
x = np.linspace(0, 10, 100)
y = 4 + 2 * np.sin(2 * x)

# plot
fig, ax = plt.subplots()

ax.plot(x, y, linewidth=2.0)

ax.set(xlim=(0, 8), xticks=np.arange(1, 8),
       ylim=(0, 8), yticks=np.arange(1, 8))

plt.show()

  1. import matplotlib.pyplot as plt: 导入Matplotlib库，并将其简化为plt，这是Matplotlib中常用的惯例。

  2. import numpy as np: 导入NumPy库，并将其简化为np，NumPy是用于数值计算的Python库。

  3. plt.style.use('_mpl-gallery'): 这里使用了一个自定义的Matplotlib样式'_mpl-gallery'。Matplotlib样式用于设置图形的外观和风格。在此之前可能有一个自定义的样式定义，但代码片段中没有显示出来。

  4. x = np.linspace(0, 10, 100): 使用NumPy的linspace函数创建一个包含100个点的等间隔数组，从0到10。这个数组将作为x轴的值。

  5. y = 4 + 2 * np.sin(2 * x): 使用NumPy的sin函数对2 * x进行正弦运算，并乘以2，然后再加上4，得到y轴的值。这个计算的结果是使y值随着x轴的增加而周期性地上下波动的一组数据。

  6. fig, ax = plt.subplots(): 创建一个图形对象和一个坐标轴对象。fig代表整个图形窗口，ax代表图形中的坐标轴。

  7. ax.plot(x, y, linewidth=2.0): 在坐标轴ax上绘制折线图，使用之前生成的x和y数组作为数据，并设置线宽为2.0。

  8. ax.set(xlim=(0, 8), xticks=np.arange(1, 8), ylim=(0, 8), yticks=np.arange(1, 8)): 设置坐标轴的范围和刻度。x轴范围设置为0到8，同时设置x轴刻度为从1到7的间隔为1的刻度。y轴范围设置为0到8，同时设置y轴刻度为从1到7的间隔为1的刻度。

  9. plt.show(): 显示绘制的图形。

plot

散点图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import matplotlib.pyplot as plt
import numpy as np

plt.style.use('_mpl-gallery')

# make the data
np.random.seed(3)
x = 4 + np.random.normal(0, 2, 24)
y = 4 + np.random.normal(0, 2, len(x))
# size and color:
sizes = np.random.uniform(15, 80, len(x))
colors = np.random.uniform(15, 80, len(x))

# plot
fig, ax = plt.subplots()

ax.scatter(x, y, s=sizes, c=colors, vmin=0, vmax=100)

ax.set(xlim=(0, 8), xticks=np.arange(1, 8),
       ylim=(0, 8), yticks=np.arange(1, 8))

plt.show()

  1. import matplotlib.pyplot as plt: 导入Matplotlib库，并将其简化为plt，这是Matplotlib中常用的惯例。

  2. import numpy as np: 导入NumPy库，并将其简化为np，NumPy是用于数值计算的Python库。

  3. plt.style.use('_mpl-gallery'): 这里使用了一个自定义的Matplotlib样式'_mpl-gallery'。Matplotlib样式用于设置图形的外观和风格。在此之前可能有一个自定义的样式定义，但代码片段中没有显示出来。

  4. np.random.seed(3): 设置随机数生成器的种子，这样每次运行代码都能得到相同的随机数据。这是为了保证结果的可复现性。

  5. x = 4 + np.random.normal(0, 2, 24): 使用NumPy的random.normal函数生成一个包含24个随机数的数组，这些随机数是从均值为0、标准差为2的正态分布中抽取的，并将每个数值都加上4。这样生成了一组带有偏移的随机数据，用作x轴的值。

  6. y = 4 + np.random.normal(0, 2, len(x)): 同样，使用NumPy的random.normal函数生成一个与x轴数据长度相同的随机数数组，并进行偏移。这样生成了一组带有偏移的随机数据，用作y轴的值。

  7. sizes = np.random.uniform(15, 80, len(x)): 使用NumPy的random.uniform函数生成一个与x轴数据长度相同的数组，其中的数值在15到80之间，用作散点的大小。

  8. colors = np.random.uniform(15, 80, len(x)): 使用NumPy的random.uniform函数生成一个与x轴数据长度相同的数组，其中的数值在15到80之间，用作散点的颜色。

  9. fig, ax = plt.subplots(): 创建一个图形对象和一个坐标轴对象。fig代表整个图形窗口，ax代表图形中的坐标轴。

  10. ax.scatter(x, y, s=sizes, c=colors, vmin=0, vmax=100): 在坐标轴ax上绘制散点图。使用之前生成的x和y数组作为数据，并使用sizes数组设置散点的大小，使用colors数组设置散点的颜色。vmin和vmax参数用于设置颜色映射范围，这里设置为0和100，即颜色范围在15到80之间。

  11. ax.set(xlim=(0, 8), xticks=np.arange(1, 8), ylim=(0, 8), yticks=np.arange(1, 8)): 设置坐标轴的范围和刻度。x轴范围设置为0到8，同时设置x轴刻度为从1到7的间隔为1的刻度。y轴范围设置为0到8，同时设置y轴刻度为从1到7的间隔为1的刻度。

  12. plt.show(): 显示绘制的图形。

scatter

条形图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import matplotlib.pyplot as plt
import numpy as np
plt.style.use('_mpl-gallery')

# make data:
x = 0.5 + np.arange(8)
y = [4.8, 5.5, 3.5, 4.6, 6.5, 6.6, 2.6, 3.0]

# plot
fig, ax = plt.subplots()

ax.bar(x, y, width=1, edgecolor="white", linewidth=0.7)

ax.set(xlim=(0, 8), xticks=np.arange(1, 8),
       ylim=(0, 8), yticks=np.arange(1, 8))

plt.show()

  1. import matplotlib.pyplot as plt: 导入Matplotlib库，并将其简化为plt，这是Matplotlib中常用的惯例。

  2. import numpy as np: 导入NumPy库，并将其简化为np，NumPy是用于数值计算的Python库。

  3. plt.style.use('_mpl-gallery'): 这里使用了一个自定义的Matplotlib样式'_mpl-gallery'。Matplotlib样式用于设置图形的外观和风格。在此之前可能有一个自定义的样式定义，但代码片段中没有显示出来。

  4. x = 0.5 + np.arange(8): 使用NumPy的arange函数生成一个从0.5开始、间隔为1的长度为8的数组。这将作为x轴的数据。

  5. y = [4.8, 5.5, 3.5, 4.6, 6.5, 6.6, 2.6, 3.0]: 定义了一个包含8个数值的列表，这些数值将作为y轴的数据。

  6. fig, ax = plt.subplots(): 创建一个图形对象和一个坐标轴对象。fig代表整个图形窗口，ax代表图形中的坐标轴。

  7. ax.bar(x, y, width=1, edgecolor="white", linewidth=0.7): 在坐标轴ax上绘制条形图。使用之前生成的x和y数组作为数据，width=1设置条形的宽度为1，edgecolor="white"设置条形的边缘颜色为白色，linewidth=0.7设置条形的边缘线宽为0.7。

  8. ax.set(xlim=(0, 8), xticks=np.arange(1, 8), ylim=(0, 8), yticks=np.arange(1, 8)): 设置坐标轴的范围和刻度。x轴范围设置为0到8，同时设置x轴刻度为从1到7的间隔为1的刻度。y轴范围设置为0到8，同时设置y轴刻度为从1到7的间隔为1的刻度。

  9. plt.show(): 显示绘制的图形。

bar

棉棒图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import matplotlib.pyplot as plt
import numpy as np

plt.style.use('_mpl-gallery')

# make data
x = 0.5 + np.arange(8)
y = [4.8, 5.5, 3.5, 4.6, 6.5, 6.6, 2.6, 3.0]

# plot
fig, ax = plt.subplots()

ax.stem(x, y)

ax.set(xlim=(0, 8), xticks=np.arange(1, 8),
       ylim=(0, 8), yticks=np.arange(1, 8))

plt.show()

  1. import matplotlib.pyplot as plt: 导入Matplotlib库，并将其简化为plt，这是Matplotlib中常用的惯例。

  2. import numpy as np: 导入NumPy库，并将其简化为np，NumPy是用于数值计算的Python库。

  3. plt.style.use('_mpl-gallery'): 这里使用了一个自定义的Matplotlib样式'_mpl-gallery'。Matplotlib样式用于设置图形的外观和风格。在此之前可能有一个自定义的样式定义，但代码片段中没有显示出来。

  4. x = 0.5 + np.arange(8): 使用NumPy的arange函数生成一个从0.5开始、间隔为1的长度为8的数组。这将作为x轴的数据。

  5. y = [4.8, 5.5, 3.5, 4.6, 6.5, 6.6, 2.6, 3.0]: 定义了一个包含8个数值的列表，这些数值将作为y轴的数据。

  6. fig, ax = plt.subplots(): 创建一个图形对象和一个坐标轴对象。fig代表整个图形窗口，ax代表图形中的坐标轴。

  7. ax.stem(x, y): 在坐标轴ax上绘制棉棒图（stem plot）。使用之前生成的x和y数组作为数据，棉棒图展示了每个x坐标对应的y值，并通过垂直线连接每个点到x轴。

  8. ax.set(xlim=(0, 8), xticks=np.arange(1, 8), ylim=(0, 8), yticks=np.arange(1, 8)): 设置坐标轴的范围和刻度。x轴范围设置为0到8，同时设置x轴刻度为从1到7的间隔为1的刻度。y轴范围设置为0到8，同时设置y轴刻度为从1到7的间隔为1的刻度。

  9. plt.show(): 显示绘制的图形。

stem

阶梯图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import matplotlib.pyplot as plt
import numpy as np

plt.style.use('_mpl-gallery')

# make data
x = 0.5 + np.arange(8)
y = [4.8, 5.5, 3.5, 4.6, 6.5, 6.6, 2.6, 3.0]

# plot
fig, ax = plt.subplots()

ax.step(x, y, linewidth=2.5)

ax.set(xlim=(0, 8), xticks=np.arange(1, 8),
       ylim=(0, 8), yticks=np.arange(1, 8))

plt.show()

  1. import matplotlib.pyplot as plt: 导入Matplotlib库，并将其简化为plt，这是Matplotlib中常用的惯例。

  2. import numpy as np: 导入NumPy库，并将其简化为np，NumPy是用于数值计算的Python库。

  3. plt.style.use('_mpl-gallery'): 这里使用了一个自定义的Matplotlib样式'_mpl-gallery'。Matplotlib样式用于设置图形的外观和风格。在此之前可能有一个自定义的样式定义，但代码片段中没有显示出来。

  4. x = 0.5 + np.arange(8): 使用NumPy的arange函数生成一个从0.5开始、间隔为1的长度为8的数组。这将作为x轴的数据。

  5. y = [4.8, 5.5, 3.5, 4.6, 6.5, 6.6, 2.6, 3.0]: 定义了一个包含8个数值的列表，这些数值将作为y轴的数据。

  6. fig, ax = plt.subplots(): 创建一个图形对象和一个坐标轴对象。fig代表整个图形窗口，ax代表图形中的坐标轴。

  7. ax.step(x, y, linewidth=2.5): 在坐标轴ax上绘制阶梯图（step plot）。使用之前生成的x和y数组作为数据，阶梯图是一种连续线段连接的图形，每个点以垂直线段连接到下一个点，形成阶梯状的线条。

  8. ax.set(xlim=(0, 8), xticks=np.arange(1, 8), ylim=(0, 8), yticks=np.arange(1, 8)): 设置坐标轴的范围和刻度。x轴范围设置为0到8，同时设置x轴刻度为从1到7的间隔为1的刻度。y轴范围设置为0到8，同时设置y轴刻度为从1到7的间隔为1的刻度。

  9. plt.show(): 显示绘制的图形。

step

填充区域图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import matplotlib.pyplot as plt
import numpy as np

plt.style.use('_mpl-gallery')

# make data
np.random.seed(1)
x = np.linspace(0, 8, 16)
y1 = 3 + 4*x/8 + np.random.uniform(0.0, 0.5, len(x))
y2 = 1 + 2*x/8 + np.random.uniform(0.0, 0.5, len(x))

# plot
fig, ax = plt.subplots()

ax.fill_between(x, y1, y2, alpha=.5, linewidth=0)
ax.plot(x, (y1 + y2)/2, linewidth=2)

ax.set(xlim=(0, 8), xticks=np.arange(1, 8),
       ylim=(0, 8), yticks=np.arange(1, 8))

plt.show()

  1. import matplotlib.pyplot as plt: 导入Matplotlib库，并将其简化为plt，这是Matplotlib中常用的惯例。

  2. import numpy as np: 导入NumPy库，并将其简化为np，NumPy是用于数值计算的Python库。

  3. plt.style.use('_mpl-gallery'): 这里使用了一个自定义的Matplotlib样式'_mpl-gallery'。Matplotlib样式用于设置图形的外观和风格。在此之前可能有一个自定义的样式定义，但代码片段中没有显示出来。

  4. np.random.seed(1): 设置随机数生成器的种子，这样每次运行代码都能得到相同的随机数据。这是为了保证结果的可复现性。

  5. x = np.linspace(0, 8, 16): 使用NumPy的linspace函数生成一个从0到8的等间隔数组，长度为16。这将作为x轴的数据。

  6. y1 = 3 + 4*x/8 + np.random.uniform(0.0, 0.5, len(x)): 使用NumPy的random.uniform函数生成一个与x轴数据长度相同的随机数数组，其中的数值在0.0到0.5之间，并将其加到3 + 4*x/8的结果中。这将生成一组y1轴的随机数据。

  7. y2 = 1 + 2*x/8 + np.random.uniform(0.0, 0.5, len(x)): 同样，使用NumPy的random.uniform函数生成一个与x轴数据长度相同的随机数数组，其中的数值在0.0到0.5之间，并将其加到1 + 2*x/8的结果中。这将生成一组y2轴的随机数据。

  8. fig, ax = plt.subplots(): 创建一个图形对象和一个坐标轴对象。fig代表整个图形窗口，ax代表图形中的坐标轴。

  9. ax.fill_between(x, y1, y2, alpha=.5, linewidth=0): 在坐标轴ax上绘制两条曲线y1和y2之间的填充区域。alpha=.5设置填充区域的透明度为0.5，linewidth=0设置填充区域的边界线宽为0，使得填充区域没有明显的边界线。

  10. ax.plot(x, (y1 + y2)/2, linewidth=2): 在坐标轴ax上绘制一条线，线的y值是y1和y2的平均值，即(y1 + y2)/2。这条线将连接y1和y2两条曲线之间填充区域的中心。

  11. ax.set(xlim=(0, 8), xticks=np.arange(1, 8), ylim=(0, 8), yticks=np.arange(1, 8)): 设置坐标轴的范围和刻度。x轴范围设置为0到8，同时设置x轴刻度为从1到7的间隔为1的刻度。y轴范围设置为0到8，同时设置y轴刻度为从1到7的间隔为1的刻度。

  12. plt.show(): 显示绘制的图形。

这段代码将绘制一个填充区域图，其中x轴的数据是从0到8的长度为16的等间隔数组，y轴的数据是通过在两个曲线y1和y2之间填充一个随机生成的小范围来得到的。填充区域由透明度为0.5的颜色填充，而中心线由y1和y2的平均值组成。x轴范围是0到8，y轴范围是0到8，并且x和y轴都有间隔为1的刻度。

fill_between

堆叠区域图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import matplotlib.pyplot as plt
import numpy as np

plt.style.use('_mpl-gallery')

# make data
x = np.arange(0, 10, 2)
ay = [1, 1.25, 2, 2.75, 3]
by = [1, 1, 1, 1, 1]
cy = [2, 1, 2, 1, 2]
y = np.vstack([ay, by, cy])

# plot
fig, ax = plt.subplots()

ax.stackplot(x, y)

ax.set(xlim=(0, 8), xticks=np.arange(1, 8),
       ylim=(0, 8), yticks=np.arange(1, 8))

plt.show()

  1. import matplotlib.pyplot as plt: 导入Matplotlib库，并将其简化为plt，这是Matplotlib中常用的惯例。

  2. import numpy as np: 导入NumPy库，并将其简化为np，NumPy是用于数值计算的Python库。

  3. plt.style.use('_mpl-gallery'): 这里使用了一个自定义的Matplotlib样式'_mpl-gallery'。Matplotlib样式用于设置图形的外观和风格。在此之前可能有一个自定义的样式定义，但代码片段中没有显示出来。

  4. x = np.arange(0, 10, 2): 使用NumPy的arange函数生成一个从0开始、间隔为2的长度为5的数组。这将作为x轴的数据。

  5. ay = [1, 1.25, 2, 2.75, 3]: 定义了一个包含5个数值的列表，这些数值将作为第一组y轴的数据。

  6. by = [1, 1, 1, 1, 1]: 定义了一个包含5个数值的列表，这些数值将作为第二组y轴的数据。

  7. cy = [2, 1, 2, 1, 2]: 定义了一个包含5个数值的列表，这些数值将作为第三组y轴的数据。

  8. y = np.vstack([ay, by, cy]): 使用NumPy的vstack函数将三组y轴数据堆叠在一起，形成一个2维数组。这样，y将成为一个包含3个子数组的数组，每个子数组代表一组y轴数据。

  9. fig, ax = plt.subplots(): 创建一个图形对象和一个坐标轴对象。fig代表整个图形窗口，ax代表图形中的坐标轴。

  10. ax.stackplot(x, y): 在坐标轴ax上绘制堆叠区域图（stacked plot）。使用之前生成的x和y数组作为数据，堆叠区域图展示了每个x坐标对应的三组y值的堆叠区域。

  11. ax.set(xlim=(0, 8), xticks=np.arange(1, 8), ylim=(0, 8), yticks=np.arange(1, 8)): 设置坐标轴的范围和刻度。x轴范围设置为0到8，同时设置x轴刻度为从1到7的间隔为1的刻度。y轴范围设置为0到8，同时设置y轴刻度为从1到7的间隔为1的刻度。

  12. plt.show(): 显示绘制的图形。

这段代码将绘制一个堆叠区域图，其中x轴的数据是从0开始的长度为5的等间隔数组，y轴的数据有三组，分别是ay、by和cy。堆叠区域图将显示三组y轴数据在每个x坐标处的堆叠区域，形成了多个不同颜色的堆叠区域。x轴范围是0到8，y轴范围是0到8，并且x和y轴都有间隔为1的刻度。

stackplot

热图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import matplotlib.pyplot as plt
import numpy as np

plt.style.use('_mpl-gallery-nogrid')

# make data
X, Y = np.meshgrid(np.linspace(-3, 3, 16), np.linspace(-3, 3, 16))
Z = (1 - X/2 + X**5 + Y**3) * np.exp(-X**2 - Y**2)

# plot
fig, ax = plt.subplots()

ax.imshow(Z)

plt.show()

  1. import matplotlib.pyplot as plt: 导入Matplotlib库，并将其简化为plt，这是Matplotlib中常用的惯例。

  2. import numpy as np: 导入NumPy库，并将其简化为np，NumPy是用于数值计算的Python库。

  3. plt.style.use('_mpl-gallery-nogrid'): 这里使用了一个自定义的Matplotlib样式'_mpl-gallery-nogrid'。Matplotlib样式用于设置图形的外观和风格。在此之前可能有一个自定义的样式定义，但代码片段中没有显示出来。

  4. X, Y = np.meshgrid(np.linspace(-3, 3, 16), np.linspace(-3, 3, 16)): 使用NumPy的meshgrid函数生成一个网格，其中X和Y分别是从-3到3的等间隔数组，长度为16。这将用于创建一个二维坐标系，其中X和Y分别表示x轴和y轴上的点。

  5. Z = (1 - X/2 + X**5 + Y**3) * np.exp(-X**2 - Y**2): 使用X和Y数组计算出一个二维数组Z，其中的数值是根据给定的函数计算得到的。这个函数是 (1 - X/2 + X**5 + Y**3) * np.exp(-X**2 - Y**2)。

  6. fig, ax = plt.subplots(): 创建一个图形对象和一个坐标轴对象。fig代表整个图形窗口，ax代表图形中的坐标轴。

  7. ax.imshow(Z): 在坐标轴ax上显示二维数组Z，这将以图像的形式显示出来。imshow函数会根据数组中的数值来着色，较大的数值将显示为较亮的颜色，较小的数值将显示为较暗的颜色。

  8. plt.show(): 显示绘制的图形。

这段代码将绘制一个基于二维数组Z的图像。Z的数值是根据给定的函数计算得到的，然后使用imshow函数将二维数组Z以图像的形式显示出来。imshow函数将根据数组中的数值自动着色，形成一个具有明暗变化的图像。在这里，Z的值由X和Y的坐标计算得到，因此图像会显示一种呈现复杂图案的分布情况。

imshow

伪彩色图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import matplotlib.pyplot as plt
import numpy as np

plt.style.use('_mpl-gallery-nogrid')

# make data with uneven sampling in x
x = [-3, -2, -1.6, -1.2, -.8, -.5, -.2, .1, .3, .5, .8, 1.1, 1.5, 1.9, 2.3, 3]
X, Y = np.meshgrid(x, np.linspace(-3, 3, 128))
Z = (1 - X/2 + X**5 + Y**3) * np.exp(-X**2 - Y**2)

# plot
fig, ax = plt.subplots()

ax.pcolormesh(X, Y, Z, vmin=-0.5, vmax=1.0)

plt.show()

  1. import matplotlib.pyplot as plt: 导入Matplotlib库，并将其简化为plt，这是Matplotlib中常用的惯例。

  2. import numpy as np: 导入NumPy库，并将其简化为np，NumPy是用于数值计算的Python库。

  3. plt.style.use('_mpl-gallery-nogrid'): 这里使用了一个自定义的Matplotlib样式'_mpl-gallery-nogrid'。Matplotlib样式用于设置图形的外观和风格。在此之前可能有一个自定义的样式定义，但代码片段中没有显示出来。

  4. x = [-3, -2, -1.6, -1.2, -.8, -.5, -.2, .1, .3, .5, .8, 1.1, 1.5, 1.9, 2.3, 3]: 定义了一个不规则的一维数组x，用于表示网格中的x坐标。这些x坐标是不均匀间隔的。

  5. X, Y = np.meshgrid(x, np.linspace(-3, 3, 128)): 使用np.meshgrid函数生成两个二维数组X和Y，其中X由不规则间隔的一维数组x和均匀间隔的一维数组np.linspace(-3, 3, 128)组成。Y由均匀间隔的一维数组np.linspace(-3, 3, 128)组成。生成的X和Y数组都是(16, 128)的形状，表示一个16行、128列的网格。

  6. Z = (1 - X/2 + X**5 + Y**3) * np.exp(-X**2 - Y**2): 这行代码计算一个二维数组Z，数组中的每个元素是通过对应位置的X和Y坐标值代入一个特定的函数表达式得到的。这个函数表达式是 (1 - X/2 + X**5 + Y**3) * np.exp(-X**2 - Y**2)。在这里，我们使用了NumPy的广播功能，X和Y是同样大小的数组，所以它们进行元素级别的运算，从而生成一个新的二维数组Z。

  7. fig, ax = plt.subplots(): 创建一个图形对象和一个坐标轴对象。fig代表整个图形窗口，ax代表图形中的坐标轴。

  8. ax.pcolormesh(X, Y, Z, vmin=-0.5, vmax=1.0): 使用ax.pcolormesh函数绘制伪彩色图。这个函数以X和Y作为网格坐标，将Z数组中的值作为颜色编码来填充网格，从而生成一个伪彩色图。vmin=-0.5和vmax=1.0分别设置了颜色编码的范围，这样可以将Z中小于-0.5的值映射为低值颜色，大于1.0的值映射为高值颜色。

  9. plt.show(): 显示绘制的图形。

这段代码将绘制一个伪彩色图，其中网格的x坐标由不规则间隔的一维数组x表示，y坐标由均匀间隔的一维数组np.linspace(-3, 3, 128)表示。在伪彩色图中，颜色编码用于表示Z数组中的值，而Z数组的值是根据特定的函数计算得到的。通过颜色的变化，我们可以直观地看到Z随着X和Y的变化而发生的变化。

这个数学公式可以写为：

$$ Z = (1 - \frac{X}{2} + X^5 + Y^3) \times e^{-X^2 - Y^2} $$

其中，$ X $ 和 $ Y $ 是网格坐标，$ Z $ 是根据 $ X $ 和 $ Y $ 计算的函数值。公式中包含了多项式和指数函数的运算。这个函数表达式用于生成一个二维数组 $ Z $，并在后续的代码中被用于绘制伪彩色图。

pcolormesh

热图（Heatmap）和伪彩色图（Pseudocolor Plot）都是用来可视化二维数据的图像表示方法，但它们在呈现数据的方式和目的上有一些区别。
热图（Heatmap）：
- 热图是一种常见的二维数据可视化方法，通常用于显示数据的分布、关联性或者密度。
- 热图使用颜色来表示数据值的大小，其中颜色的明暗程度代表数据的相对大小。
- 通常，较大的数值用较深的颜色表示，较小的数值用较浅的颜色表示，从而形成一个明暗变化的色阶。
- 热图通常用于展示数据的整体结构和趋势，以及在不同位置的数据值之间的相对大小关系。
- 例子：在基因表达数据分析中，热图可以用来显示不同基因在不同样本中的表达量，帮助研究基因的表达模式。
伪彩色图（Pseudocolor Plot）：
- 伪彩色图也是一种二维数据可视化方法，用于表示数据的变化和分布情况。
- 伪彩色图使用颜色来编码数据的数值，不同颜色代表不同数值，而不仅仅是数据的大小。
- 伪彩色图通常用于展示数据的细节和变化，以及在不同位置的具体数值。
- 通常，可以通过设定颜色映射范围来控制颜色的分配，从而突出数据的特定范围或变化。
- 例子：在物理模拟中，伪彩色图可以用来显示模拟结果的数值，例如温度分布、流速等。
总体而言，热图更适合呈现数据的总体结构和相对关系，而伪彩色图更适合呈现数据的具体数值和细节变化。但在某些情况下，这两种图形方法可以相互转换或混用，具体要根据数据的特性和可视化的目的来选择适合的方法。

等高线图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import matplotlib.pyplot as plt
import numpy as np

plt.style.use('_mpl-gallery-nogrid')

# make data
X, Y = np.meshgrid(np.linspace(-3, 3, 256), np.linspace(-3, 3, 256))
Z = (1 - X/2 + X**5 + Y**3) * np.exp(-X**2 - Y**2)
levels = np.linspace(np.min(Z), np.max(Z), 7)

# plot
fig, ax = plt.subplots()

ax.contour(X, Y, Z, levels=levels)

plt.show()

  1. import matplotlib.pyplot as plt: 导入Matplotlib库，并将其简化为plt，这是Matplotlib中常用的惯例。

  2. import numpy as np: 导入NumPy库，并将其简化为np，NumPy是用于数值计算的Python库。

  3. plt.style.use('_mpl-gallery-nogrid'): 这里使用了一个自定义的Matplotlib样式'_mpl-gallery-nogrid'。Matplotlib样式用于设置图形的外观和风格。在此之前可能有一个自定义的样式定义，但代码片段中没有显示出来。

  4. X, Y = np.meshgrid(np.linspace(-3, 3, 256), np.linspace(-3, 3, 256)): 使用np.meshgrid函数生成两个二维数组X和Y，其中X由均匀间隔的一维数组np.linspace(-3, 3, 256)组成，Y也是由均匀间隔的一维数组np.linspace(-3, 3, 256)组成。生成的X和Y数组都是(256, 256)的形状，表示一个256x256的网格。

  5. Z = (1 - X/2 + X**5 + Y**3) * np.exp(-X**2 - Y**2): 这行代码计算一个二维数组Z，数组中的每个元素是通过对应位置的X和Y坐标值代入一个特定的函数表达式得到的。这个函数表达式是 (1 - X/2 + X**5 + Y**3) * np.exp(-X**2 - Y**2)。在这里，我们使用了NumPy的广播功能，X和Y是同样大小的数组，所以它们进行元素级别的运算，从而生成一个新的二维数组Z。

  6. levels = np.linspace(np.min(Z), np.max(Z), 7): 创建一个包含7个元素的一维数组levels，其中的数值是通过等间隔方式从Z数组的最小值到最大值生成的。这些数值将用于设置等高线图中的轮廓线的高度值。

  7. fig, ax = plt.subplots(): 创建一个图形对象和一个坐标轴对象。fig代表整个图形窗口，ax代表图形中的坐标轴。

  8. ax.contour(X, Y, Z, levels=levels): 使用ax.contour函数绘制等高线图。这个函数以X和Y作为网格坐标，将Z数组中的值作为高度值来绘制等高线。通过设置levels参数，等高线图将在指定的高度值处绘制轮廓线。

  9. plt.show(): 显示绘制的图形。

这段代码将绘制一个等高线图，其中网格的x坐标由均匀间隔的一维数组np.linspace(-3, 3, 256)表示，y坐标也由均匀间隔的一维数组np.linspace(-3, 3, 256)表示。在等高线图中，不同高度值对应的轮廓线将呈现出数据的变化和分布情况。通过观察轮廓线的分布和形状，我们可以了解函数在二维空间中的变化和特性。

contour

填充等高线图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import matplotlib.pyplot as plt
import numpy as np

plt.style.use('_mpl-gallery-nogrid')

# make data
X, Y = np.meshgrid(np.linspace(-3, 3, 256), np.linspace(-3, 3, 256))
Z = (1 - X/2 + X**5 + Y**3) * np.exp(-X**2 - Y**2)
levels = np.linspace(Z.min(), Z.max(), 7)

# plot
fig, ax = plt.subplots()

ax.contourf(X, Y, Z, levels=levels)

plt.show()

  1. import matplotlib.pyplot as plt: 导入Matplotlib库，并将其简化为plt，这是Matplotlib中常用的惯例。

  2. import numpy as np: 导入NumPy库，并将其简化为np，NumPy是用于数值计算的Python库。

  3. plt.style.use('_mpl-gallery-nogrid'): 这里使用了一个自定义的Matplotlib样式'_mpl-gallery-nogrid'。Matplotlib样式用于设置图形的外观和风格。在此之前可能有一个自定义的样式定义，但代码片段中没有显示出来。

  4. X, Y = np.meshgrid(np.linspace(-3, 3, 256), np.linspace(-3, 3, 256)): 使用np.meshgrid函数生成两个二维数组X和Y，其中X由均匀间隔的一维数组np.linspace(-3, 3, 256)组成，Y也是由均匀间隔的一维数组np.linspace(-3, 3, 256)组成。生成的X和Y数组都是(256, 256)的形状，表示一个256x256的网格。

  5. Z = (1 - X/2 + X**5 + Y**3) * np.exp(-X**2 - Y**2): 这行代码计算一个二维数组Z，数组中的每个元素是通过对应位置的X和Y坐标值代入一个特定的函数表达式得到的。这个函数表达式是 (1 - X/2 + X**5 + Y**3) * np.exp(-X**2 - Y**2)。在这里，我们使用了NumPy的广播功能，X和Y是同样大小的数组，所以它们进行元素级别的运算，从而生成一个新的二维数组Z。

  6. levels = np.linspace(Z.min(), Z.max(), 7): 创建一个包含7个元素的一维数组levels，其中的数值是通过等间隔方式从Z数组的最小值到最大值生成的。这些数值将用于设置填充等高线图中的色块的高度值。

  7. fig, ax = plt.subplots(): 创建一个图形对象和一个坐标轴对象。fig代表整个图形窗口，ax代表图形中的坐标轴。

  8. ax.contourf(X, Y, Z, levels=levels): 使用ax.contourf函数绘制填充等高线图。这个函数以X和Y作为网格坐标，将Z数组中的值作为高度值来绘制填充等高线图。通过设置levels参数，填充等高线图将在指定的高度值处绘制色块。

  9. plt.show(): 显示绘制的图形。

这段代码将绘制一个填充等高线图，其中网格的x坐标由均匀间隔的一维数组np.linspace(-3, 3, 256)表示，y坐标也由均匀间隔的一维数组np.linspace(-3, 3, 256)表示。在填充等高线图中，不同高度值对应的色块将呈现出数据的变化和分布情况，填充等高线图比普通的等高线图更突出数据的整体结构和趋势。通过观察色块的分布和形状，我们可以直观地了解函数在二维空间中的变化和特性。

contourf

风羽图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import matplotlib.pyplot as plt
import numpy as np

plt.style.use('_mpl-gallery-nogrid')

# make data:
X, Y = np.meshgrid([1, 2, 3, 4], [1, 2, 3, 4])
angle = np.pi / 180 * np.array([[15., 30, 35, 45],
                                [25., 40, 55, 60],
                                [35., 50, 65, 75],
                                [45., 60, 75, 90]])
amplitude = np.array([[5, 10, 25, 50],
                      [10, 15, 30, 60],
                      [15, 26, 50, 70],
                      [20, 45, 80, 100]])
U = amplitude * np.sin(angle)
V = amplitude * np.cos(angle)

# plot:
fig, ax = plt.subplots()

ax.barbs(X, Y, U, V, barbcolor='C0', flagcolor='C0', length=7, linewidth=1.5)

ax.set(xlim=(0, 4.5), ylim=(0, 4.5))

plt.show()

  1. import matplotlib.pyplot as plt: 导入Matplotlib库，并将其简化为plt，这是Matplotlib中常用的惯例。

  2. import numpy as np: 导入NumPy库，并将其简化为np，NumPy是用于数值计算的Python库。

  3. plt.style.use('_mpl-gallery-nogrid'): 这里使用了一个自定义的Matplotlib样式'_mpl-gallery-nogrid'。Matplotlib样式用于设置图形的外观和风格。在此之前可能有一个自定义的样式定义，但代码片段中没有显示出来。

  4. X, Y = np.meshgrid([1, 2, 3, 4], [1, 2, 3, 4]): 使用np.meshgrid函数生成两个二维数组X和Y，其中X由一维数组[1, 2, 3, 4]组成，Y也由一维数组[1, 2, 3, 4]组成。生成的X和Y数组都是(4, 4)的形状，表示一个4x4的网格，用于表示风羽图中的位置。

  5. angle和amplitude分别是两个(4, 4)的二维数组，分别表示风的角度（方向）和风速的大小。这些数据用于计算风的速度在x和y方向的分量，分别保存在U和V数组中。

  6. U = amplitude * np.sin(angle): 这行代码计算风速在x方向的分量。

  7. V = amplitude * np.cos(angle): 这行代码计算风速在y方向的分量。

  8. fig, ax = plt.subplots(): 创建一个图形对象和一个坐标轴对象。fig代表整个图形窗口，ax代表图形中的坐标轴。

  9. ax.barbs(X, Y, U, V, barbcolor='C0', flagcolor='C0', length=7, linewidth=1.5): 使用ax.barbs函数绘制风羽图。这个函数以X和Y作为网格坐标，U和V分别作为风速在x和y方向的分量。barbcolor参数设置风羽的颜色，flagcolor参数设置风羽旗帜的颜色，length参数设置风羽的长度，linewidth参数设置风羽的线宽。

  10. ax.set(xlim=(0, 4.5), ylim=(0, 4.5)): 设置坐标轴的显示范围，以便风羽图完整显示在图形中。

  11. plt.show(): 显示绘制的图形。

这段代码将绘制一个风羽图，其中风的方向和风速由angle和amplitude数组表示。风羽图中的每个风羽表示了风的方向和大小。风速越大，风羽的长度越长；风的方向由风羽的方向表示。通过观察风羽图，我们可以直观地了解风的分布和风向的变化。

barbs

矢量场图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import matplotlib.pyplot as plt
import numpy as np

plt.style.use('_mpl-gallery-nogrid')

# make data
x = np.linspace(-4, 4, 6)
y = np.linspace(-4, 4, 6)
X, Y = np.meshgrid(x, y)
U = X + Y
V = Y - X

# plot
fig, ax = plt.subplots()

ax.quiver(X, Y, U, V, color="C0", angles='xy',
          scale_units='xy', scale=5, width=.015)

ax.set(xlim=(-5, 5), ylim=(-5, 5))

plt.show()

  1. import matplotlib.pyplot as plt: 导入Matplotlib库，并将其简化为plt，这是Matplotlib中常用的惯例。

  2. import numpy as np: 导入NumPy库，并将其简化为np，NumPy是用于数值计算的Python库。

  3. plt.style.use('_mpl-gallery-nogrid'): 这里使用了一个自定义的Matplotlib样式'_mpl-gallery-nogrid'。Matplotlib样式用于设置图形的外观和风格。在此之前可能有一个自定义的样式定义，但代码片段中没有显示出来。

  4. x = np.linspace(-4, 4, 6): 使用np.linspace函数创建一个包含6个均匀分布的点的数组，范围从-4到4。这个数组用于表示x轴上的坐标点。

  5. y = np.linspace(-4, 4, 6): 使用np.linspace函数创建一个包含6个均匀分布的点的数组，范围从-4到4。这个数组用于表示y轴上的坐标点。

  6. X, Y = np.meshgrid(x, y): 使用np.meshgrid函数生成两个二维数组X和Y，分别表示所有x轴和y轴坐标点的组合。在这个例子中，X和Y都是(6, 6)的形状，表示一个6x6的网格。

  7. U = X + Y: 这行代码计算矢量场中每个点的x轴分量。在这个例子中，x轴分量 U 是X和Y的和。

  8. V = Y - X: 这行代码计算矢量场中每个点的y轴分量。在这个例子中，y轴分量 V 是Y减去X。

  9. fig, ax = plt.subplots(): 创建一个图形对象和一个坐标轴对象。fig代表整个图形窗口，ax代表图形中的坐标轴。

  10. ax.quiver(X, Y, U, V, color="C0", angles='xy', scale_units='xy', scale=5, width=.015): 使用ax.quiver函数绘制矢量场图。这个函数以X和Y作为网格坐标，U和V分别作为矢量场中每个点的x轴和y轴分量。color="C0"设置箭头的颜色为蓝色，angles='xy'表示箭头是使用x和y坐标轴来表示角度，scale_units='xy'表示箭头的比例尺是相对于x和y坐标轴的单位，scale=5设置箭头的比例尺为5，width=.015设置箭头的宽度为0.015。

  11. ax.set(xlim=(-5, 5), ylim=(-5, 5)): 设置坐标轴的显示范围，以便矢量场图完整显示在图形中。

  12. plt.show(): 显示绘制的图形。

这段代码将绘制一个矢量场图，其中每个箭头表示矢量场中的一个点。箭头的位置由X和Y数组确定，箭头的方向和大小由U和V数组决定。箭头的方向表示在每个点的x和y方向上的分量，箭头的长度和宽度则决定了箭头的大小。通过观察矢量场图，我们可以直观地了解矢量场在不同位置的方向和大小。

quiver

流线图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import matplotlib.pyplot as plt
import numpy as np

plt.style.use('_mpl-gallery-nogrid')

# make a stream function:
X, Y = np.meshgrid(np.linspace(-3, 3, 256), np.linspace(-3, 3, 256))
Z = (1 - X/2 + X**5 + Y**3) * np.exp(-X**2 - Y**2)
# make U and V out of the streamfunction:
V = np.diff(Z[1:, :], axis=1)
U = -np.diff(Z[:, 1:], axis=0)

# plot:
fig, ax = plt.subplots()

ax.streamplot(X[1:, 1:], Y[1:, 1:], U, V)

plt.show()

  1. import matplotlib.pyplot as plt: 导入Matplotlib库，并将其简化为plt，这是Matplotlib中常用的惯例。

  2. import numpy as np: 导入NumPy库，并将其简化为np，NumPy是用于数值计算的Python库。

  3. plt.style.use('_mpl-gallery-nogrid'): 这里使用了一个自定义的Matplotlib样式'_mpl-gallery-nogrid'。Matplotlib样式用于设置图形的外观和风格。在此之前可能有一个自定义的样式定义，但代码片段中没有显示出来。

  4. X, Y = np.meshgrid(np.linspace(-3, 3, 256), np.linspace(-3, 3, 256)): 使用np.meshgrid函数生成两个二维数组X和Y，分别表示从-3到3范围内均匀分布的256个点的网格。这些数组将用于表示流场中的坐标点。

  5. Z = (1 - X/2 + X**5 + Y**3) * np.exp(-X**2 - Y**2): 这行代码计算流函数 Z。流函数是一个标量场函数，它通常用于描述流体流动的速度分布。在这个例子中，Z 是根据给定的公式计算得到的，它是关于 X 和 Y 的函数。

  6. V = np.diff(Z[1:, :], axis=1): 这行代码计算速度场中每个点的y轴分量。在这个例子中，y轴分量 V 是 Z 数组在y方向上的差分。

  7. U = -np.diff(Z[:, 1:], axis=0): 这行代码计算速度场中每个点的x轴分量。在这个例子中，x轴分量 U 是 Z 数组在x方向上的差分，注意差分得到的结果要取负号。

  8. fig, ax = plt.subplots(): 创建一个图形对象和一个坐标轴对象。fig代表整个图形窗口，ax代表图形中的坐标轴。

  9. ax.streamplot(X[1:, 1:], Y[1:, 1:], U, V): 使用ax.streamplot函数绘制流线图。这个函数以 X[1:, 1:] 和 Y[1:, 1:] 作为网格坐标，U 和 V 作为速度场中每个点的x轴和y轴分量。streamplot函数会根据速度场的信息绘制出流线，并展示流体在给定流场中的运动。

  10. plt.show(): 显示绘制的图形。

这段代码将绘制一个流线图，其中流线表示在给定的流场中流体的运动情况。流线的分布和形态展示了流体在该流场中的运动轨迹和速度分布。通过观察流线图，我们可以了解流体在不同位置的运动方向和速度。

streamplot

直方图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import matplotlib.pyplot as plt
import numpy as np

plt.style.use('_mpl-gallery')

# make data
np.random.seed(1)
x = 4 + np.random.normal(0, 1.5, 200)

# plot:
fig, ax = plt.subplots()

ax.hist(x, bins=8, linewidth=0.5, edgecolor="white")

ax.set(xlim=(0, 8), xticks=np.arange(1, 8),
       ylim=(0, 56), yticks=np.linspace(0, 56, 9))

plt.show()

  1. import matplotlib.pyplot as plt: 导入Matplotlib库，并将其简化为plt，这是Matplotlib中常用的惯例。

  2. import numpy as np: 导入NumPy库，并将其简化为np，NumPy是用于数值计算的Python库。

  3. plt.style.use('_mpl-gallery'): 这里使用了一个自定义的Matplotlib样式'_mpl-gallery'。Matplotlib样式用于设置图形的外观和风格。在此之前可能有一个自定义的样式定义，但代码片段中没有显示出来。

  4. np.random.seed(1): 设置随机数种子，保证每次运行代码生成的随机数据都是一样的，便于复现结果。

  5. x = 4 + np.random.normal(0, 1.5, 200): 使用np.random.normal生成一个包含200个随机数的数据集 x。这些随机数是从均值为4、标准差为1.5的正态分布中随机抽取的。

  6. fig, ax = plt.subplots(): 创建一个图形对象和一个坐标轴对象。fig代表整个图形窗口，ax代表图形中的坐标轴。

  7. ax.hist(x, bins=8, linewidth=0.5, edgecolor="white"): 使用ax.hist函数绘制直方图。该函数以数据集 x 为输入，bins=8指定了直方图的箱数为8，即直方图将被分成8个箱子，linewidth=0.5设置直方图边界线的宽度为0.5，edgecolor="white"设置直方图边界线的颜色为白色。

  8. ax.set(xlim=(0, 8), xticks=np.arange(1, 8), ylim=(0, 56), yticks=np.linspace(0, 56, 9)): 使用ax.set方法设置坐标轴的显示范围和刻度。xlim=(0, 8)设置x轴显示范围为0到8，xticks=np.arange(1, 8)设置x轴刻度为从1到7的整数刻度，ylim=(0, 56)设置y轴显示范围为0到56，yticks=np.linspace(0, 56, 9)设置y轴刻度为0到56之间等间距的9个刻度。

  9. plt.show(): 显示绘制的图形。

这段代码将绘制一个直方图，其中每个箱子表示数据集 x 在相应范围内的数据个数。通过观察直方图，我们可以了解数据集 x 的分布情况，以及数据在不同区间的频次分布。直方图是一种常用的数据可视化方法，用于对数据进行初步的统计和分布分析。

hist

箱线图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import matplotlib.pyplot as plt
import numpy as np

plt.style.use('_mpl-gallery')

# make data:
np.random.seed(10)
D = np.random.normal((3, 5, 4), (1.25, 1.00, 1.25), (100, 3))

# plot
fig, ax = plt.subplots()
VP = ax.boxplot(D, positions=[2, 4, 6], widths=1.5, patch_artist=True,
                showmeans=False, showfliers=False,
                medianprops={"color": "white", "linewidth": 0.5},
                boxprops={"facecolor": "C0", "edgecolor": "white",
                          "linewidth": 0.5},
                whiskerprops={"color": "C0", "linewidth": 1.5},
                capprops={"color": "C0", "linewidth": 1.5})

ax.set(xlim=(0, 8), xticks=np.arange(1, 8),
       ylim=(0, 8), yticks=np.arange(1, 8))

plt.show()

  1. import matplotlib.pyplot as plt: 导入Matplotlib库，并将其简化为plt，这是Matplotlib中常用的惯例。

  2. import numpy as np: 导入NumPy库，并将其简化为np，NumPy是用于数值计算的Python库。

  3. plt.style.use('_mpl-gallery'): 这里使用了一个自定义的Matplotlib样式'_mpl-gallery'。Matplotlib样式用于设置图形的外观和风格。在此之前可能有一个自定义的样式定义，但代码片段中没有显示出来。

  4. np.random.seed(10): 设置随机数种子，保证每次运行代码生成的随机数据都是一样的，便于复现结果。

  5. D = np.random.normal((3, 5, 4), (1.25, 1.00, 1.25), (100, 3)): 使用np.random.normal生成三个包含100个随机数的数据集，每个数据集对应一个正态分布。其中 (3, 5, 4) 是均值，(1.25, 1.00, 1.25) 是标准差，(100, 3) 是生成的数据集的形状。

  6. fig, ax = plt.subplots(): 创建一个图形对象和一个坐标轴对象。fig代表整个图形窗口，ax代表图形中的坐标轴。

  7. ax.boxplot(D, positions=[2, 4, 6], widths=1.5, patch_artist=True, ...)：使用ax.boxplot函数绘制箱线图。D 是要绘制的数据集，positions=[2, 4, 6] 设置了每个箱线图的位置，即将三个数据集绘制在x轴上的位置为2、4和6。widths=1.5 设置了每个箱线图的宽度为1.5。patch_artist=True 设置箱体用填充方式绘制。showmeans=False 和 showfliers=False 分别设置不显示均值和离群值。medianprops、boxprops、whiskerprops 和 capprops 参数用于设置箱线图中各个部分的属性，例如箱体、中位数线、箱须线和箱顶线的颜色和宽度。

  8. ax.set(xlim=(0, 8), xticks=np.arange(1, 8), ylim=(0, 8), yticks=np.arange(1, 8)): 使用ax.set方法设置坐标轴的显示范围和刻度。xlim=(0, 8)设置x轴显示范围为0到8，xticks=np.arange(1, 8)设置x轴刻度为从1到7的整数刻度，ylim=(0, 8)设置y轴显示范围为0到8，yticks=np.arange(1, 8)设置y轴刻度为从1到7的整数刻度。

  9. plt.show(): 显示绘制的图形。

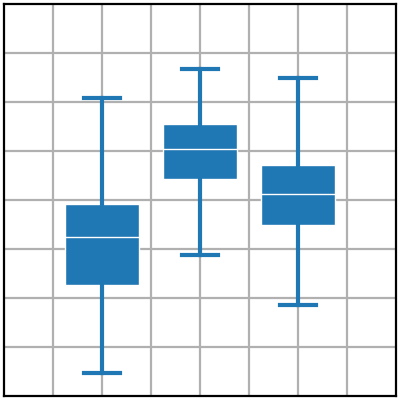
这段代码将绘制一个箱线图，其中每个箱线图表示一个数据集的分布情况。箱线图展示了数据的中位数、上下四分位数和离群值等统计特征，可以帮助我们快速了解数据的分布和异常值情况。

箱线图是一种常用的数据可视化工具，用于展示数据的分布情况和离群值。通过观察箱线图，你可以了解数据的中位数、四分位数、离群值等统计信息，从而更好地理解数据的整体分布和异常情况。

以下是如何看箱线图的一些方法：

  1. 箱体： 箱线图的主要部分是箱体，它表示数据的四分位数范围。箱体的底边界和顶边界分别对应第一四分位数（Q1）和第三四分位数（Q3）。箱体的中间线表示中位数（Q2），即数据的中值。箱体的高度反映了数据的离散程度，越高表示数据的变异性越大。

  2. 箱须线： 箱线图的箱须线延伸出箱体，表示数据的范围。上边的箱须线通常表示数据中的最大值（除去离群值），下边的箱须线表示数据中的最小值（除去离群值）。箱须线可以帮助你了解数据的整体范围。

  3. 离群值： 离群值是指数据中明显偏离其他数据的值。在箱线图中，通常将离群值单独表示为散点或小圆圈。离群值可能是数据中的异常值，也可能表示了数据的特殊情况。通过观察离群值，你可以判断数据中是否存在异常或特殊的观测值。

  4. 比较箱线图： 如果有多个数据集的箱线图在同一张图中显示，你可以通过比较它们来观察数据的差异和共性。比较不同箱线图可以帮助你发现数据之间的异同，以及是否存在某种趋势或模式。

  5. 偏态和尾重： 箱线图也可以用来观察数据的偏态（Skewness）和尾重（Heavy Tails）。偏态表示数据分布的不对称程度，正偏态表示数据右侧较长，负偏态表示数据左侧较长。尾重表示数据分布的尾部概率密度较大，尾部的概率分布比较重。

  6. 异常检测： 箱线图可以用于识别数据中的异常值。通常，超出箱须线的数据点可能是离群值或异常值，值得注意和进一步调查。

通过合理观察和解释箱线图的各个元素，你可以得到关于数据分布、偏态、异常值等方面的直观认识，并从中获取对数据的洞察和见解。

boxplot

误差线图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import matplotlib.pyplot as plt
import numpy as np

plt.style.use('_mpl-gallery')

# make data:
np.random.seed(1)
x = [2, 4, 6]
y = [3.6, 5, 4.2]
yerr = [0.9, 1.2, 0.5]

# plot:
fig, ax = plt.subplots()

ax.errorbar(x, y, yerr, fmt='o', linewidth=2, capsize=6)

ax.set(xlim=(0, 8), xticks=np.arange(1, 8),
       ylim=(0, 8), yticks=np.arange(1, 8))

plt.show()

  1. import matplotlib.pyplot as plt: 导入Matplotlib库，并将其简化为plt，这是Matplotlib中常用的惯例。

  2. import numpy as np: 导入NumPy库，并将其简化为np，NumPy是用于数值计算的Python库。

  3. plt.style.use('_mpl-gallery'): 这里使用了一个自定义的Matplotlib样式'_mpl-gallery'。Matplotlib样式用于设置图形的外观和风格。在此之前可能有一个自定义的样式定义，但代码片段中没有显示出来。

  4. np.random.seed(1): 设置随机数种子，保证每次运行代码生成的随机数据都是一样的，便于复现结果。

  5. x = [2, 4, 6]: 定义一个包含3个x坐标的列表。

  6. y = [3.6, 5, 4.2]: 定义一个包含3个y坐标的列表，这些y坐标表示在相应x位置上的测量值。

  7. yerr = [0.9, 1.2, 0.5]: 定义一个包含3个y误差的列表，表示在相应x位置上的测量值的误差范围。

  8. fig, ax = plt.subplots(): 创建一个图形对象和一个坐标轴对象。fig代表整个图形窗口，ax代表图形中的坐标轴。

  9. ax.errorbar(x, y, yerr, fmt='o', linewidth=2, capsize=6): 使用ax.errorbar函数绘制带有误差线的散点图。x和y是散点的横纵坐标数据，yerr是y方向的误差范围。fmt='o'指定散点的形状为圆点，linewidth=2设置误差线的宽度为2，capsize=6设置误差线两端的横线长度为6。

  10. ax.set(xlim=(0, 8), xticks=np.arange(1, 8), ylim=(0, 8), yticks=np.arange(1, 8)): 使用ax.set方法设置坐标轴的显示范围和刻度。xlim=(0, 8)设置x轴显示范围为0到8，xticks=np.arange(1, 8)设置x轴刻度为从1到7的整数刻度，ylim=(0, 8)设置y轴显示范围为0到8，yticks=np.arange(1, 8)设置y轴刻度为从1到7的整数刻度。

  11. plt.show(): 显示绘制的图形。

这段代码将绘制一个带有误差线的散点图，其中每个散点表示在相应x位置上的测量值，误差线表示了在相应x位置上的测量值的误差范围。带误差线的散点图可以帮助我们了解数据的可靠性和测量误差。

errorbar

小提琴图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import matplotlib.pyplot as plt
import numpy as np

plt.style.use('_mpl-gallery')

# make data:
np.random.seed(10)
D = np.random.normal((3, 5, 4), (0.75, 1.00, 0.75), (200, 3))

# plot:
fig, ax = plt.subplots()

vp = ax.violinplot(D, [2, 4, 6], widths=2,
                   showmeans=False, showmedians=False, showextrema=False)
# styling:
for body in vp['bodies']:
    body.set_alpha(0.9)
ax.set(xlim=(0, 8), xticks=np.arange(1, 8),
       ylim=(0, 8), yticks=np.arange(1, 8))

plt.show()

  1. import matplotlib.pyplot as plt: 导入Matplotlib库，并将其简化为plt，这是Matplotlib中常用的惯例。

  2. import numpy as np: 导入NumPy库，并将其简化为np，NumPy是用于数值计算的Python库。

  3. plt.style.use('_mpl-gallery'): 这里使用了一个自定义的Matplotlib样式'_mpl-gallery'。Matplotlib样式用于设置图形的外观和风格。在此之前可能有一个自定义的样式定义，但代码片段中没有显示出来。

  4. np.random.seed(10): 设置随机数种子，保证每次运行代码生成的随机数据都是一样的，便于复现结果。

  5. D = np.random.normal((3, 5, 4), (0.75, 1.00, 0.75), (200, 3)): 使用np.random.normal生成三组包含200个随机数的数据集，每组数据集对应一个正态分布。其中 (3, 5, 4) 是均值，(0.75, 1.00, 0.75) 是标准差，(200, 3) 是生成的数据集的形状。

  6. fig, ax = plt.subplots(): 创建一个图形对象和一个坐标轴对象。fig代表整个图形窗口，ax代表图形中的坐标轴。

  7. vp = ax.violinplot(D, [2, 4, 6], widths=2, showmeans=False, showmedians=False, showextrema=False): 使用ax.violinplot函数绘制小提琴图。D 是要绘制的数据集，[2, 4, 6] 设置了每个小提琴图的位置，即将三个数据集绘制在x轴上的位置为2、4和6。widths=2 设置了小提琴图的宽度为2。showmeans=False、showmedians=False 和 showextrema=False 分别设置不显示均值、中位数和极值线。小提琴图通过核密度估计展示了数据的分布情况。

  8. for body in vp['bodies']: body.set_alpha(0.9): 对小提琴图的主体进行样式设置，将其透明度设置为0.9。

  9. ax.set(xlim=(0, 8), xticks=np.arange(1, 8), ylim=(0, 8), yticks=np.arange(1, 8)): 使用ax.set方法设置坐标轴的显示范围和刻度。xlim=(0, 8)设置x轴显示范围为0到8，xticks=np.arange(1, 8)设置x轴刻度为从1到7的整数刻度，ylim=(0, 8)设置y轴显示范围为0到8，yticks=np.arange(1, 8)设置y轴刻度为从1到7的整数刻度。

  10. plt.show(): 显示绘制的图形。

这段代码将绘制三个小提琴图，每个小提琴图代表一个数据集的分布情况。小提琴图可以帮助我们直观地了解数据的分布及其密度，从而更好地理解数据集的特征和统计属性。

violinplot

事件图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import matplotlib.pyplot as plt
import numpy as np

plt.style.use('_mpl-gallery')

# make data:
np.random.seed(1)
x = [2, 4, 6]
D = np.random.gamma(4, size=(3, 50))

# plot:
fig, ax = plt.subplots()

ax.eventplot(D, orientation="vertical", lineoffsets=x, linewidth=0.75)

ax.set(xlim=(0, 8), xticks=np.arange(1, 8),
       ylim=(0, 8), yticks=np.arange(1, 8))

plt.show()

  1. import matplotlib.pyplot as plt: 导入Matplotlib库，并将其简化为plt，这是Matplotlib中常用的惯例。

  2. import numpy as np: 导入NumPy库，并将其简化为np，NumPy是用于数值计算的Python库。

  3. plt.style.use('_mpl-gallery'): 这里使用了一个自定义的Matplotlib样式'_mpl-gallery'。Matplotlib样式用于设置图形的外观和风格。在此之前可能有一个自定义的样式定义，但代码片段中没有显示出来。

  4. np.random.seed(1): 设置随机数种子，保证每次运行代码生成的随机数据都是一样的，便于复现结果。

  5. x = [2, 4, 6]: 定义一个包含3个x坐标的列表。

  6. D = np.random.gamma(4, size=(3, 50)): 使用np.random.gamma生成三个数据集，每个数据集包含50个从Gamma分布中随机生成的值。Gamma分布是一种常见的概率分布，它在许多领域中都有应用。

  7. fig, ax = plt.subplots(): 创建一个图形对象和一个坐标轴对象。fig代表整个图形窗口，ax代表图形中的坐标轴。

  8. ax.eventplot(D, orientation="vertical", lineoffsets=x, linewidth=0.75): 使用ax.eventplot函数绘制事件图。D 是要绘制的数据集，orientation="vertical" 指定事件图的方向为垂直方向。lineoffsets=x 设置了事件图的x坐标位置，即将三个数据集绘制在x轴上的位置为2、4和6。linewidth=0.75 设置事件图的线宽为0.75。

  9. ax.set(xlim=(0, 8), xticks=np.arange(1, 8), ylim=(0, 8), yticks=np.arange(1, 8)): 使用ax.set方法设置坐标轴的显示范围和刻度。xlim=(0, 8)设置x轴显示范围为0到8，xticks=np.arange(1, 8)设置x轴刻度为从1到7的整数刻度，ylim=(0, 8)设置y轴显示范围为0到8，yticks=np.arange(1, 8)设置y轴刻度为从1到7的整数刻度。

  10. plt.show(): 显示绘制的图形。

这段代码将绘制三个事件图，每个事件图代表一个数据集的事件发生情况。事件图可以用于可视化数据中的事件发生次数或发生时间，帮助我们了解数据的分布和事件之间的关联性。

eventplot

二维直方图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import matplotlib.pyplot as plt
import numpy as np

plt.style.use('_mpl-gallery-nogrid')

# make data: correlated + noise
np.random.seed(1)
x = np.random.randn(5000)
y = 1.2 * x + np.random.randn(5000) / 3

# plot:
fig, ax = plt.subplots()

ax.hist2d(x, y, bins=(np.arange(-3, 3, 0.1), np.arange(-3, 3, 0.1)))

ax.set(xlim=(-2, 2), ylim=(-3, 3))

plt.show()

  1. import matplotlib.pyplot as plt: 导入Matplotlib库，并将其简化为plt，这是Matplotlib中常用的惯例。

  2. import numpy as np: 导入NumPy库，并将其简化为np，NumPy是用于数值计算的Python库。

  3. plt.style.use('_mpl-gallery-nogrid'): 这里使用了一个自定义的Matplotlib样式'_mpl-gallery-nogrid'。Matplotlib样式用于设置图形的外观和风格。在此之前可能有一个自定义的样式定义，但代码片段中没有显示出来。

  4. np.random.seed(1): 设置随机数种子，保证每次运行代码生成的随机数据都是一样的，便于复现结果。

  5. x = np.random.randn(5000): 生成一个包含5000个随机数的数组x，这些随机数是从标准正态分布（均值为0，标准差为1）中生成的。

  6. y = 1.2 * x + np.random.randn(5000) / 3: 生成一个包含5000个随机数的数组y，其中y与x具有一定的线性相关性，并添加了一些噪声。具体地，y是由x线性变换得到，并加上了从标准正态分布中随机生成的噪声，噪声的标准差为1/3。

  7. fig, ax = plt.subplots(): 创建一个图形对象和一个坐标轴对象。fig代表整个图形窗口，ax代表图形中的坐标轴。

  8. ax.hist2d(x, y, bins=(np.arange(-3, 3, 0.1), np.arange(-3, 3, 0.1))): 使用ax.hist2d函数绘制二维直方图。x和y是要绘制的二维数据，bins设置了直方图的区间范围和分箱数目。在这里，x和y的区间范围都是从-3到3，分箱数目为60（(3-(-3)) / 0.1 = 60）。

  9. ax.set(xlim=(-2, 2), ylim=(-3, 3)): 使用ax.set方法设置坐标轴的显示范围。xlim=(-2, 2)设置x轴显示范围为-2到2，ylim=(-3, 3)设置y轴显示范围为-3到3。

  10. plt.show(): 显示绘制的图形。

这段代码将绘制一个二维直方图，用于展示两个变量x和y之间的相关性和分布情况。二维直方图可以帮助我们直观地了解两个变量之间的关系和分布特征，尤其适用于观察大量数据点的情况。在直方图中，颜色越深表示数据点越密集，颜色越浅表示数据点较少。

hist2d

六边形图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import matplotlib.pyplot as plt
import numpy as np

plt.style.use('_mpl-gallery-nogrid')

# make data: correlated + noise
np.random.seed(1)
x = np.random.randn(5000)
y = 1.2 * x + np.random.randn(5000) / 3

# plot:
fig, ax = plt.subplots()

ax.hexbin(x, y, gridsize=20)

ax.set(xlim=(-2, 2), ylim=(-3, 3))

plt.show()

  1. import matplotlib.pyplot as plt: 导入Matplotlib库，并将其简化为plt，这是Matplotlib中常用的惯例。

  2. import numpy as np: 导入NumPy库，并将其简化为np，NumPy是用于数值计算的Python库。

  3. plt.style.use('_mpl-gallery-nogrid'): 这里使用了一个自定义的Matplotlib样式'_mpl-gallery-nogrid'。Matplotlib样式用于设置图形的外观和风格。在此之前可能有一个自定义的样式定义，但代码片段中没有显示出来。

  4. np.random.seed(1): 设置随机数种子，保证每次运行代码生成的随机数据都是一样的，便于复现结果。

  5. x = np.random.randn(5000): 生成一个包含5000个随机数的数组x，这些随机数是从标准正态分布（均值为0，标准差为1）中生成的。

  6. y = 1.2 * x + np.random.randn(5000) / 3: 生成一个包含5000个随机数的数组y，其中y与x具有一定的线性相关性，并添加了一些噪声。具体地，y是由x线性变换得到，并加上了从标准正态分布中随机生成的噪声，噪声的标准差为1/3。

  7. fig, ax = plt.subplots(): 创建一个图形对象和一个坐标轴对象。fig代表整个图形窗口，ax代表图形中的坐标轴。

  8. ax.hexbin(x, y, gridsize=20): 使用ax.hexbin函数绘制六边形图。x和y是要绘制的二维数据，gridsize=20设置了六边形的网格大小。该参数控制了六边形的大小和密度，数值越大，表示六边形的大小越小、密度越大。

  9. ax.set(xlim=(-2, 2), ylim=(-3, 3)): 使用ax.set方法设置坐标轴的显示范围。xlim=(-2, 2)设置x轴显示范围为-2到2，ylim=(-3, 3)设置y轴显示范围为-3到3。

  10. plt.show(): 显示绘制的图形。

这段代码将绘制一个六边形图，用于展示两个变量x和y之间的相关性和分布情况。六边形图在处理大量数据点时有着较好的可视化效果，可以帮助我们更好地理解两个变量之间的关系和分布特征。在图中，六边形的颜色深浅表示数据点的密集程度，颜色越深表示数据点越密集。

hexbin

饼图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import matplotlib.pyplot as plt
import numpy as np

plt.style.use('_mpl-gallery-nogrid')


# make data
x = [1, 2, 3, 4]
colors = plt.get_cmap('Blues')(np.linspace(0.2, 0.7, len(x)))

# plot
fig, ax = plt.subplots()
ax.pie(x, colors=colors, radius=3, center=(4, 4),
       wedgeprops={"linewidth": 1, "edgecolor": "white"}, frame=True)

ax.set(xlim=(0, 8), xticks=np.arange(1, 8),
       ylim=(0, 8), yticks=np.arange(1, 8))

plt.show()

  1. import matplotlib.pyplot as plt: 导入Matplotlib库，并将其简化为plt，这是Matplotlib中常用的惯例。

  2. import numpy as np: 导入NumPy库，并将其简化为np，NumPy是用于数值计算的Python库。

  3. plt.style.use('_mpl-gallery-nogrid'): 这里使用了一个自定义的Matplotlib样式'_mpl-gallery-nogrid'。Matplotlib样式用于设置图形的外观和风格。在此之前可能有一个自定义的样式定义，但代码片段中没有显示出来。

  4. x = [1, 2, 3, 4]: 定义了一个包含4个数据点的列表x，每个数据点表示饼图中的一个扇区。

  5. colors = plt.get_cmap('Blues')(np.linspace(0.2, 0.7, len(x))): 使用plt.get_cmap('Blues')函数获取一个蓝色调色板，np.linspace(0.2, 0.7, len(x))用于生成一个0.2到0.7的等差数列，长度与数据点个数相同。这些数值用于定义扇区的颜色，颜色逐渐从浅蓝到深蓝。

  6. fig, ax = plt.subplots(): 创建一个图形对象和一个坐标轴对象。fig代表整个图形窗口，ax代表图形中的坐标轴。

  7. ax.pie(x, colors=colors, radius=3, center=(4, 4), wedgeprops={"linewidth": 1, "edgecolor": "white"}, frame=True): 使用ax.pie函数绘制饼图。x是要绘制的数据，colors=colors用于设置扇区的颜色，radius=3设置饼图的半径为3个单位，center=(4, 4)设置饼图的中心位置为坐标(4, 4)处，wedgeprops={"linewidth": 1, "edgecolor": "white"}用于设置扇区边界的线宽和颜色，frame=True表示显示饼图的边框。

  8. ax.set(xlim=(0, 8), xticks=np.arange(1, 8), ylim=(0, 8), yticks=np.arange(1, 8)): 使用ax.set方法设置坐标轴的显示范围和刻度位置。xlim=(0, 8)设置x轴显示范围为0到8，xticks=np.arange(1, 8)设置x轴的刻度位置为1到7，ylim=(0, 8)设置y轴显示范围为0到8，yticks=np.arange(1, 8)设置y轴的刻度位置为1到7。

  9. plt.show(): 显示绘制的图形。

这段代码将绘制一个饼图，用于展示一组数据的占比情况。每个数据点对应饼图中的一个扇区，扇区的面积表示该数据点在总体中的占比。颜色从浅蓝到深蓝逐渐变化，用于区分不同的数据点。饼图是一种常用的可视化方式，适用于展示不同类别在总体中的比例关系。

pie

三角剖分等高线图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import matplotlib.pyplot as plt
import numpy as np

plt.style.use('_mpl-gallery-nogrid')

# make data:
np.random.seed(1)
x = np.random.uniform(-3, 3, 256)
y = np.random.uniform(-3, 3, 256)
z = (1 - x/2 + x**5 + y**3) * np.exp(-x**2 - y**2)
levels = np.linspace(z.min(), z.max(), 7)

# plot:
fig, ax = plt.subplots()

ax.plot(x, y, 'o', markersize=2, color='lightgrey')
ax.tricontour(x, y, z, levels=levels)

ax.set(xlim=(-3, 3), ylim=(-3, 3))

plt.show()

  1. import matplotlib.pyplot as plt: 导入Matplotlib库，并将其简化为plt，这是Matplotlib中常用的惯例。

  2. import numpy as np: 导入NumPy库，并将其简化为np，NumPy是用于数值计算的Python库。

  3. plt.style.use('_mpl-gallery-nogrid'): 这里使用了一个自定义的Matplotlib样式'_mpl-gallery-nogrid'。Matplotlib样式用于设置图形的外观和风格。在此之前可能有一个自定义的样式定义，但代码片段中没有显示出来。

  4. np.random.seed(1): 设置随机数种子，保证每次运行代码生成的随机数据都是一样的，便于复现结果。

  5. x = np.random.uniform(-3, 3, 256): 生成一个包含256个随机数的数组x，这些随机数是从-3到3的均匀分布中生成的。

  6. y = np.random.uniform(-3, 3, 256): 生成一个包含256个随机数的数组y，这些随机数是从-3到3的均匀分布中生成的。

  7. z = (1 - x/2 + x**5 + y**3) * np.exp(-x**2 - y**2): 生成一个包含256个随机数的数组z，其中z是通过对x、y进行一系列数学运算得到的。具体地，z是通过以下公式计算得到的：z = (1 - x/2 + x5 + y3) * np.exp(-x2 - y2)。

  8. levels = np.linspace(z.min(), z.max(), 7): 使用np.linspace函数生成一个包含7个数值的等差数列，这些数值在z的最小值和最大值之间。

  9. fig, ax = plt.subplots(): 创建一个图形对象和一个坐标轴对象。fig代表整个图形窗口，ax代表图形中的坐标轴。

  10. ax.plot(x, y, 'o', markersize=2, color='lightgrey'): 使用ax.plot函数绘制原始数据点。在这里，将x、y作为散点图绘制在图中，并使用'o'表示散点形状为圆圈，markersize=2设置散点的大小为2个单位，color='lightgrey'设置散点的颜色为浅灰色。

  11. ax.tricontour(x, y, z, levels=levels): 使用ax.tricontour函数绘制三角剖分等高线图。x、y是原始数据点的坐标，z是对应的高度值，levels=levels用于设置等高线的数值。

  12. ax.set(xlim=(-3, 3), ylim=(-3, 3)): 使用ax.set方法设置坐标轴的显示范围。xlim=(-3, 3)设置x轴显示范围为-3到3，ylim=(-3, 3)设置y轴显示范围为-3到3。

  13. plt.show(): 显示绘制的图形。

这段代码将绘制一个三角剖分等高线图，用于展示二维数据在三维空间中的等高线分布情况。三角剖分等高线图适用于处理在不规则网格上的数据点，可以更准确地表示数据的分布情况，并帮助我们理解数据的变化趋势。

tricontour

填充三角剖分等高线图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import matplotlib.pyplot as plt
import numpy as np

plt.style.use('_mpl-gallery-nogrid')

# make data:
np.random.seed(1)
x = np.random.uniform(-3, 3, 256)
y = np.random.uniform(-3, 3, 256)
z = (1 - x/2 + x**5 + y**3) * np.exp(-x**2 - y**2)
levels = np.linspace(z.min(), z.max(), 7)

# plot:
fig, ax = plt.subplots()

ax.plot(x, y, 'o', markersize=2, color='grey')
ax.tricontourf(x, y, z, levels=levels)

ax.set(xlim=(-3, 3), ylim=(-3, 3))

plt.show()

  1. import matplotlib.pyplot as plt: 导入Matplotlib库，并将其简化为plt，这是Matplotlib中常用的惯例。

  2. import numpy as np: 导入NumPy库，并将其简化为np，NumPy是用于数值计算的Python库。

  3. plt.style.use('_mpl-gallery-nogrid'): 这里使用了一个自定义的Matplotlib样式'_mpl-gallery-nogrid'。Matplotlib样式用于设置图形的外观和风格。在此之前可能有一个自定义的样式定义，但代码片段中没有显示出来。

  4. np.random.seed(1): 设置随机数种子，保证每次运行代码生成的随机数据都是一样的，便于复现结果。

  5. x = np.random.uniform(-3, 3, 256): 生成一个包含256个随机数的数组x，这些随机数是从-3到3的均匀分布中生成的。

  6. y = np.random.uniform(-3, 3, 256): 生成一个包含256个随机数的数组y，这些随机数是从-3到3的均匀分布中生成的。

  7. z = (1 - x/2 + x**5 + y**3) * np.exp(-x**2 - y**2): 生成一个包含256个随机数的数组z，其中z是通过对x、y进行一系列数学运算得到的。具体地，z是通过以下公式计算得到的：z = (1 - x/2 + x5 + y3) * np.exp(-x2 - y2)。

  8. levels = np.linspace(z.min(), z.max(), 7): 使用np.linspace函数生成一个包含7个数值的等差数列，这些数值在z的最小值和最大值之间。

  9. fig, ax = plt.subplots(): 创建一个图形对象和一个坐标轴对象。fig代表整个图形窗口，ax代表图形中的坐标轴。

  10. ax.plot(x, y, 'o', markersize=2, color='grey'): 使用ax.plot函数绘制原始数据点。在这里，将x、y作为散点图绘制在图中，并使用'o'表示散点形状为圆圈，markersize=2设置散点的大小为2个单位，color='grey'设置散点的颜色为灰色。

  11. ax.tricontourf(x, y, z, levels=levels): 使用ax.tricontourf函数绘制填充三角剖分等高线图。x、y是原始数据点的坐标，z是对应的高度值，levels=levels用于设置等高线的数值，并且使用填充颜色表示等高线区域。

  12. ax.set(xlim=(-3, 3), ylim=(-3, 3)): 使用ax.set方法设置坐标轴的显示范围。xlim=(-3, 3)设置x轴显示范围为-3到3，ylim=(-3, 3)设置y轴显示范围为-3到3。

  13. plt.show(): 显示绘制的图形。

这段代码将绘制一个填充三角剖分等高线图，用于展示二维数据在三维空间中的等高线分布情况，并通过填充颜色来强调不同高度区域的差异。填充三角剖分等高线图适用于处理在不规则网格上的数据点，并且通过填充颜色可以更直观地表示数据的变化趋势。

tricontourf

三角剖分彩色图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import matplotlib.pyplot as plt
import numpy as np

plt.style.use('_mpl-gallery-nogrid')

# make data:
np.random.seed(1)
x = np.random.uniform(-3, 3, 256)
y = np.random.uniform(-3, 3, 256)
z = (1 - x/2 + x**5 + y**3) * np.exp(-x**2 - y**2)

# plot:
fig, ax = plt.subplots()

ax.plot(x, y, 'o', markersize=2, color='grey')
ax.tripcolor(x, y, z)

ax.set(xlim=(-3, 3), ylim=(-3, 3))

plt.show()

  1. import matplotlib.pyplot as plt: 导入Matplotlib库，并将其简化为plt，这是Matplotlib中常用的惯例。

  2. import numpy as np: 导入NumPy库，并将其简化为np，NumPy是用于数值计算的Python库。

  3. plt.style.use('_mpl-gallery-nogrid'): 这里使用了一个自定义的Matplotlib样式'_mpl-gallery-nogrid'。Matplotlib样式用于设置图形的外观和风格。在此之前可能有一个自定义的样式定义，但代码片段中没有显示出来。

  4. np.random.seed(1): 设置随机数种子，保证每次运行代码生成的随机数据都是一样的，便于复现结果。

  5. x = np.random.uniform(-3, 3, 256): 生成一个包含256个随机数的数组x，这些随机数是从-3到3的均匀分布中生成的。

  6. y = np.random.uniform(-3, 3, 256): 生成一个包含256个随机数的数组y，这些随机数是从-3到3的均匀分布中生成的。

  7. z = (1 - x/2 + x**5 + y**3) * np.exp(-x**2 - y**2): 生成一个包含256个随机数的数组z，其中z是通过对x、y进行一系列数学运算得到的。具体地，z是通过以下公式计算得到的：z = (1 - x/2 + x5 + y3) * np.exp(-x2 - y2)。

  8. fig, ax = plt.subplots(): 创建一个图形对象和一个坐标轴对象。fig代表整个图形窗口，ax代表图形中的坐标轴。

  9. ax.plot(x, y, 'o', markersize=2, color='grey'): 使用ax.plot函数绘制原始数据点。在这里，将x、y作为散点图绘制在图中，并使用'o'表示散点形状为圆圈，markersize=2设置散点的大小为2个单位，color='grey'设置散点的颜色为灰色。

  10. ax.tripcolor(x, y, z): 使用ax.tripcolor函数绘制三角剖分彩色图。x、y是原始数据点的坐标，z是对应的高度值，函数将根据数据点的三角剖分情况来着色，形成彩色的三角区域。

  11. ax.set(xlim=(-3, 3), ylim=(-3, 3)): 使用ax.set方法设置坐标轴的显示范围。xlim=(-3, 3)设置x轴显示范围为-3到3，ylim=(-3, 3)设置y轴显示范围为-3到3。

  12. plt.show(): 显示绘制的图形。

这段代码将绘制一个三角剖分彩色图，用于展示二维数据在三维空间中的变化情况，并通过彩色表示不同高度区域的差异。三角剖分彩色图适用于处理在不规则网格上的数据点，并且通过彩色能够更直观地表示数据的变化趋势。

tripcolor

三角剖分图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import matplotlib.pyplot as plt
import numpy as np

plt.style.use('_mpl-gallery-nogrid')

# make data:
np.random.seed(1)
x = np.random.uniform(-3, 3, 256)
y = np.random.uniform(-3, 3, 256)
z = (1 - x/2 + x**5 + y**3) * np.exp(-x**2 - y**2)

# plot:
fig, ax = plt.subplots()

ax.triplot(x, y)

ax.set(xlim=(-3, 3), ylim=(-3, 3))

plt.show()

  1. import matplotlib.pyplot as plt: 导入Matplotlib库，并将其简化为plt，这是Matplotlib中常用的惯例。

  2. import numpy as np: 导入NumPy库，并将其简化为np，NumPy是用于数值计算的Python库。

  3. plt.style.use('_mpl-gallery-nogrid'): 这里使用了一个自定义的Matplotlib样式'_mpl-gallery-nogrid'。Matplotlib样式用于设置图形的外观和风格。在此之前可能有一个自定义的样式定义，但代码片段中没有显示出来。

  4. np.random.seed(1): 设置随机数种子，保证每次运行代码生成的随机数据都是一样的，便于复现结果。

  5. x = np.random.uniform(-3, 3, 256): 生成一个包含256个随机数的数组x，这些随机数是从-3到3的均匀分布中生成的。

  6. y = np.random.uniform(-3, 3, 256): 生成一个包含256个随机数的数组y，这些随机数是从-3到3的均匀分布中生成的。

  7. z = (1 - x/2 + x**5 + y**3) * np.exp(-x**2 - y**2): 生成一个包含256个随机数的数组z，其中z是通过对x、y进行一系列数学运算得到的。具体地，z是通过以下公式计算得到的：z = (1 - x/2 + x5 + y3) * np.exp(-x2 - y2)。

  8. fig, ax = plt.subplots(): 创建一个图形对象和一个坐标轴对象。fig代表整个图形窗口，ax代表图形中的坐标轴。

  9. ax.triplot(x, y): 使用ax.triplot函数绘制三角剖分图。x、y是原始数据点的坐标，函数会根据这些数据点之间的三角剖分关系绘制三角网格。

  10. ax.set(xlim=(-3, 3), ylim=(-3, 3)): 使用ax.set方法设置坐标轴的显示范围。xlim=(-3, 3)设置x轴显示范围为-3到3，ylim=(-3, 3)设置y轴显示范围为-3到3。

  11. plt.show(): 显示绘制的图形。

这段代码将绘制一个三角剖分图，用于展示二维数据在三维空间中的数据点之间的三角剖分关系。三角剖分图适用于处理在不规则网格上的数据点，并且通过三角网格可以更直观地表示数据点之间的连接关系。

triplot

三维散点图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import matplotlib.pyplot as plt
import numpy as np

plt.style.use('_mpl-gallery')

# Make data
np.random.seed(19680801)
n = 100
rng = np.random.default_rng()
xs = rng.uniform(23, 32, n)
ys = rng.uniform(0, 100, n)
zs = rng.uniform(-50, -25, n)

# Plot
fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
ax.scatter(xs, ys, zs)

ax.set(xticklabels=[],
       yticklabels=[],
       zticklabels=[])

plt.show()

  1. import matplotlib.pyplot as plt: 导入Matplotlib库，并将其简化为plt，这是Matplotlib中常用的惯例。

  2. import numpy as np: 导入NumPy库，并将其简化为np，NumPy是用于数值计算的Python库。

  3. plt.style.use('_mpl-gallery'): 这里使用了一个自定义的Matplotlib样式'_mpl-gallery'。Matplotlib样式用于设置图形的外观和风格。在此之前可能有一个自定义的样式定义，但代码片段中没有显示出来。

  4. np.random.seed(19680801): 设置随机数种子，保证每次运行代码生成的随机数据都是一样的，便于复现结果。

  5. n = 100: 定义数据点的数量。

  6. rng = np.random.default_rng(): 创建一个随机数生成器对象。

  7. xs = rng.uniform(23, 32, n): 用随机数生成器生成包含100个随机数的数组xs，这些随机数是从23到32的均匀分布中生成的。

  8. ys = rng.uniform(0, 100, n): 用随机数生成器生成包含100个随机数的数组ys，这些随机数是从0到100的均匀分布中生成的。

  9. zs = rng.uniform(-50, -25, n): 用随机数生成器生成包含100个随机数的数组zs，这些随机数是从-50到-25的均匀分布中生成的。

  10. fig, ax = plt.subplots(subplot_kw={"projection": "3d"}): 创建一个带有三维坐标轴的图形对象和一个三维坐标轴对象。fig代表整个图形窗口，ax代表图形中的三维坐标轴。

  11. ax.scatter(xs, ys, zs): 使用ax.scatter函数绘制三维散点图。xs、ys、zs是数据点的x、y、z坐标，函数会在三维坐标轴上绘制这些数据点。

  12. ax.set(xticklabels=[], yticklabels=[], zticklabels=[]): 设置三维坐标轴的刻度标签为空，这样就隐藏了x、y、z轴的刻度标签。

  13. plt.show(): 显示绘制的图形。

这段代码绘制了一个简单的三维散点图，其中包含了100个随机生成的数据点，用于展示数据在三维空间中的分布情况。

scatter

三维曲面图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import matplotlib.pyplot as plt
from matplotlib import cm
import numpy as np

plt.style.use('_mpl-gallery')

# Make data
X = np.arange(-5, 5, 0.25)
Y = np.arange(-5, 5, 0.25)
X, Y = np.meshgrid(X, Y)
R = np.sqrt(X**2 + Y**2)
Z = np.sin(R)

# Plot the surface
fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
ax.plot_surface(X, Y, Z, vmin=Z.min() * 2, cmap=cm.Blues)

ax.set(xticklabels=[],
       yticklabels=[],
       zticklabels=[])

plt.show()

  1. import matplotlib.pyplot as plt: 导入Matplotlib库，并将其简化为plt，这是Matplotlib中常用的惯例。

  2. from matplotlib import cm: 从Matplotlib库中导入cm，用于获取颜色映射(colormap)。

  3. plt.style.use('_mpl-gallery'): 这里使用了一个自定义的Matplotlib样式'_mpl-gallery'。Matplotlib样式用于设置图形的外观和风格。在此之前可能有一个自定义的样式定义，但代码片段中没有显示出来。

  4. X = np.arange(-5, 5, 0.25): 创建一个包含从-5到5的间隔为0.25的一维数组X。

  5. Y = np.arange(-5, 5, 0.25): 创建一个包含从-5到5的间隔为0.25的一维数组Y。

  6. X, Y = np.meshgrid(X, Y): 将X和Y组合成一个二维网格，生成X和Y的二维数组，分别表示X和Y坐标的网格。

  7. R = np.sqrt(X**2 + Y**2): 计算每个点到原点(0,0)的距离，得到一个二维数组R。

  8. Z = np.sin(R): 计算每个点的正弦值，得到一个二维数组Z。

  9. fig, ax = plt.subplots(subplot_kw={"projection": "3d"}): 创建一个带有三维坐标轴的图形对象和一个三维坐标轴对象。fig代表整个图形窗口，ax代表图形中的三维坐标轴。

  10. ax.plot_surface(X, Y, Z, vmin=Z.min() * 2, cmap=cm.Blues): 使用ax.plot_surface函数绘制三维曲面图。X、Y、Z分别表示数据点的x、y、z坐标，函数会根据这些坐标在三维坐标轴上绘制曲面。vmin参数设置颜色映射的最小值，这里将其设置为Z.min() * 2，即z值的最小值的两倍。cmap=cm.Blues设置颜色映射为蓝色调。

  11. ax.set(xticklabels=[], yticklabels=[], zticklabels=[]): 设置三维坐标轴的刻度标签为空，这样就隐藏了x、y、z轴的刻度标签。

  12. plt.show(): 显示绘制的图形。

这段代码绘制了一个包含正弦函数在二维平面上的三维曲面图，颜色随着z值的变化而变化，呈现出蓝色调的效果。

plot_surface

三维三角网面图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
import matplotlib.pyplot as plt
from matplotlib import cm
import numpy as np

plt.style.use('_mpl-gallery')

n_radii = 8
n_angles = 36

# Make radii and angles spaces
radii = np.linspace(0.125, 1.0, n_radii)
angles = np.linspace(0, 2*np.pi, n_angles, endpoint=False)[..., np.newaxis]

# Convert polar (radii, angles) coords to cartesian (x, y) coords.
x = np.append(0, (radii*np.cos(angles)).flatten())
y = np.append(0, (radii*np.sin(angles)).flatten())
z = np.sin(-x*y)

# Plot
fig, ax = plt.subplots(subplot_kw={'projection': '3d'})
ax.plot_trisurf(x, y, z, vmin=z.min() * 2, cmap=cm.Blues)

ax.set(xticklabels=[],
       yticklabels=[],
       zticklabels=[])

plt.show()

  1. import matplotlib.pyplot as plt: 导入Matplotlib库，并将其简化为plt，这是Matplotlib中常用的惯例。

  2. from matplotlib import cm: 从Matplotlib库中导入cm，用于获取颜色映射(colormap)。

  3. plt.style.use('_mpl-gallery'): 这里使用了一个自定义的Matplotlib样式'_mpl-gallery'。Matplotlib样式用于设置图形的外观和风格。在此之前可能有一个自定义的样式定义，但代码片段中没有显示出来。

  4. n_radii = 8: 定义半径的数量。

  5. n_angles = 36: 定义角度的数量。

  6. radii = np.linspace(0.125, 1.0, n_radii): 创建一个包含8个均匀间隔的半径值的一维数组radii，范围从0.125到1.0。

  7. angles = np.linspace(0, 2*np.pi, n_angles, endpoint=False)[..., np.newaxis]: 创建一个包含36个均匀间隔的角度值的一维数组angles，范围从0到2π，每个角度值都用一个维度表示。

  8. x = np.append(0, (radii*np.cos(angles)).flatten()): 计算x坐标值，radii*np.cos(angles)将极坐标转换为直角坐标，并使用flatten()将二维数组展平成一维数组。然后通过np.append()函数在数组的开头插入0，以使得曲面图在原点处闭合。

  9. y = np.append(0, (radii*np.sin(angles)).flatten()): 计算y坐标值，radii*np.sin(angles)将极坐标转换为直角坐标，并使用flatten()将二维数组展平成一维数组。然后通过np.append()函数在数组的开头插入0，以使得曲面图在原点处闭合。

  10. z = np.sin(-x*y): 计算z坐标值，根据x和y的值计算z的值，这里使用了正弦函数。

  11. fig, ax = plt.subplots(subplot_kw={'projection': '3d'}): 创建一个带有三维坐标轴的图形对象和一个三维坐标轴对象。fig代表整个图形窗口，ax代表图形中的三维坐标轴。

  12. ax.plot_trisurf(x, y, z, vmin=z.min() * 2, cmap=cm.Blues): 使用ax.plot_trisurf函数绘制三维三角网面图。x、y、z分别表示数据点的x、y、z坐标，函数会根据这些坐标在三维坐标轴上绘制三角网面图。vmin参数设置颜色映射的最小值，这里将其设置为z.min() * 2，即z值的最小值的两倍。cmap=cm.Blues设置颜色映射为蓝色调。

  13. ax.set(xticklabels=[], yticklabels=[], zticklabels=[]): 设置三维坐标轴的刻度标签为空，这样就隐藏了x、y、z轴的刻度标签。

  14. plt.show(): 显示绘制的图形。

这段代码绘制了一个在极坐标系下的三维三角网面图，颜色随着z值的变化而变化，呈现出蓝色调的效果。

plot_trisurf

三维体素图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import matplotlib.pyplot as plt
import numpy as np

plt.style.use('_mpl-gallery')

# Prepare some coordinates
x, y, z = np.indices((8, 8, 8))

# Draw cuboids in the top left and bottom right corners
cube1 = (x < 3) & (y < 3) & (z < 3)
cube2 = (x >= 5) & (y >= 5) & (z >= 5)

# Combine the objects into a single boolean array
voxelarray = cube1 | cube2

# Plot
fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
ax.voxels(voxelarray, edgecolor='k')

ax.set(xticklabels=[],
       yticklabels=[],
       zticklabels=[])

plt.show()

  1. import matplotlib.pyplot as plt: 导入Matplotlib库，并将其简化为plt，这是Matplotlib中常用的惯例。

  2. plt.style.use('_mpl-gallery'): 这里使用了一个自定义的Matplotlib样式'_mpl-gallery'。Matplotlib样式用于设置图形的外观和风格。在此之前可能有一个自定义的样式定义，但代码片段中没有显示出来。

  3. x, y, z = np.indices((8, 8, 8)): 创建了一个3D坐标网格，其中x、y和z坐标都取值范围为0到7。这样可以得到一个8x8x8的三维网格。

  4. cube1 = (x < 3) & (y < 3) & (z < 3): 创建了一个立方体1，它包含了坐标点(x, y, z)满足x < 3、y < 3和z < 3的所有点。

  5. cube2 = (x >= 5) & (y >= 5) & (z >= 5): 创建了一个立方体2，它包含了坐标点(x, y, z)满足x >= 5、y >= 5和z >= 5的所有点。

  6. voxelarray = cube1 | cube2: 将立方体1和立方体2组合成一个单一的布尔数组voxelarray。在这个数组中，值为True的元素表示在立方体内，值为False的元素表示在立方体外。

  7. fig, ax = plt.subplots(subplot_kw={"projection": "3d"}): 创建一个带有三维坐标轴的图形对象和一个三维坐标轴对象。fig代表整个图形窗口，ax代表图形中的三维坐标轴。

  8. ax.voxels(voxelarray, edgecolor='k'): 使用ax.voxels函数绘制三维体素图。voxelarray表示要绘制的体素的布尔数组，edgecolor='k'设置体素的边缘颜色为黑色。

  9. ax.set(xticklabels=[], yticklabels=[], zticklabels=[]): 设置三维坐标轴的刻度标签为空，这样就隐藏了x、y、z轴的刻度标签。

  10. plt.show(): 显示绘制的图形。

这段代码绘制了一个简单的三维体素图，其中包含两个立方体。其中一个立方体位于三维空间的左上角，另一个立方体位于右下角。

voxels

三维线框图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt

plt.style.use('_mpl-gallery')

# Make data
X, Y, Z = axes3d.get_test_data(0.05)

# Plot
fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
ax.plot_wireframe(X, Y, Z, rstride=10, cstride=10)

ax.set(xticklabels=[],
       yticklabels=[],
       zticklabels=[])

plt.show()

  1. from mpl_toolkits.mplot3d import axes3d: 导入Matplotlib中的axes3d模块，这个模块包含了用于绘制三维图形的函数和工具。

  2. import matplotlib.pyplot as plt: 导入Matplotlib库，并将其简化为plt，这是Matplotlib中常用的惯例。

  3. plt.style.use('_mpl-gallery'): 这里使用了一个自定义的Matplotlib样式'_mpl-gallery'。Matplotlib样式用于设置图形的外观和风格。在此之前可能有一个自定义的样式定义，但代码片段中没有显示出来。

  4. X, Y, Z = axes3d.get_test_data(0.05): 使用axes3d.get_test_data()函数获取测试数据。这个函数返回了一个包含X、Y、Z坐标数据的三维网格，用于绘制一个三维曲面。0.05是步长参数，控制数据的稠密程度。

  5. fig, ax = plt.subplots(subplot_kw={"projection": "3d"}): 创建一个带有三维坐标轴的图形对象和一个三维坐标轴对象。fig代表整个图形窗口，ax代表图形中的三维坐标轴。

  6. ax.plot_wireframe(X, Y, Z, rstride=10, cstride=10): 使用ax.plot_wireframe()函数绘制三维线框图。X、Y、Z是三维曲面的坐标数据，rstride和cstride分别控制行和列的采样步长，用于控制曲面的稠密程度。

  7. ax.set(xticklabels=[], yticklabels=[], zticklabels=[]): 设置三维坐标轴的刻度标签为空，这样就隐藏了x、y、z轴的刻度标签。

  8. plt.show(): 显示绘制的图形。

这段代码绘制了一个三维线框图，该图显示了一个曲面的结构，曲面的形状基于获取的测试数据。三维线框图通过连接数据点之间的线条来表示曲面的形状，使得可以更好地了解曲面的结构和特征。

plot_wireframe
Python Matplotlib
Prev:
DecisionTree算法简析
Next:
KNN算法简析

    • Copyright © 2023 - 2024 kclx | Powered by Hexo | Theme Bamboo