期末复习-数据导入与预处理

AdaBoost算法简析

概述

AdaBoost（Adaptive Boosting）是一种集成学习（Ensemble Learning）算法，旨在提高分类算法的性能。它通过将多个弱分类器（通常是简单的、性能略优于随机猜测的分类器）组合在一起，形成一个强分类器，从而实现更准确的分类。

以下是AdaBoost算法的概述：

1. 数据准备： 首先，需要准备带有标签的训练数据集，其中每个样本都有一个已知的类别标签。

2. 初始化权重： 对每个样本赋予一个初始权重，这些权重表示样本在训练过程中的重要性。通常情况下，初始权重相等。

3. 迭代训练： AdaBoost通过一系列迭代来构建强分类器。在每次迭代中，它执行以下步骤：

   a. 选择弱分类器： 从一组可能的弱分类器中选择一个，该选择是基于当前样本权重和分类器的性能来做出的。

   b. 训练弱分类器： 使用当前样本权重对选择的弱分类器进行训练，使其在当前数据分布下尽可能准确地分类。

   c. 计算错误率： 计算弱分类器在当前数据分布下的错误率，以便在下一步中进行权重调整。

   d. 更新样本权重： 根据弱分类器的错误率调整样本权重，增加被错误分类的样本的权重，降低被正确分类的样本的权重。

4. 组合弱分类器： 对于每个迭代步骤，都会为弱分类器分配一个权重，该权重基于其性能。然后，将所有弱分类器的结果按照权重加权组合起来，形成一个强分类器。

5. 分类预测： 使用构建的强分类器来进行新样本的分类预测。强分类器将根据每个弱分类器的权重对样本进行分类，最终输出最可能的类别标签。

AdaBoost的关键思想在于每一次迭代都会调整样本的权重，将注意力集中在被错误分类的样本上，从而逐步改善分类性能。最终，通过组合多个弱分类器，AdaBoost能够产生一个在分类任务中表现良好的强分类器。

需要注意的是，AdaBoost对异常值比较敏感，因此在使用时需要谨慎处理数据异常情况。另外，AdaBoost在一些特定情况下可能会过拟合，因此可能需要进行适当的调参或者尝试其他集成学习方法。

AdaBoost与RandomForest

AdaBoost（Adaptive Boosting）和Random Forest都是集成学习算法，用于提高分类算法的性能。它们有一些共同之处，但也存在一些显著的区别。下面是它们之间的主要区别与联系：

区别：

1. 基本分类器的选择：

   • AdaBoost：AdaBoost的基本分类器是弱分类器，通常是一个简单的分类器，如决策树的深度很小。
   • Random Forest：Random Forest的基本分类器是决策树，通常是深度较大的决策树。

2. 样本权重：

   • AdaBoost：AdaBoost在每次迭代中调整样本的权重，将注意力集中在被错误分类的样本上。
   • Random Forest：Random Forest不调整样本权重，每棵决策树都基于原始数据进行训练。

3. 训练方式：

   • AdaBoost：AdaBoost是通过顺序迭代的方式构建弱分类器，并逐步提高其性能。
   • Random Forest：Random Forest是通过并行训练多棵决策树，每棵树都在随机抽取的子样本上进行训练，然后对它们的预测结果进行投票或平均。

4. 权重分配：

   • AdaBoost：AdaBoost在构建最终分类器时，对每个弱分类器分配一个权重，用于组合它们的预测结果。
   • Random Forest：Random Forest对所有决策树的预测结果进行投票（分类问题）或平均（回归问题），最终确定最终结果。

联系：

1. 集成思想： AdaBoost和Random Forest都采用了集成学习的思想，通过组合多个基本分类器来提高整体性能。

2. 减少过拟合： 两种算法都能有效减少过拟合的风险。AdaBoost通过调整样本权重来关注难以分类的样本，而Random Forest通过随机子样本和特征选择来增加模型的多样性，从而减少过拟合。

3. 应用领域： 两种算法在各种应用领域都有广泛的应用，包括分类和回归问题。

4. 模型解释： 通常情况下，Random Forest的模型比较容易解释，因为它由多个决策树组成。相比之下，由于AdaBoost使用加权投票组合多个弱分类器，解释起来可能稍微复杂一些。

在选择使用AdaBoost还是Random Forest时，你需要考虑数据特点、问题复杂度以及模型性能等因素。需要注意的是，这两种算法并不是适用于所有问题的通用解决方案，有时候其他的集成学习方法或单一模型可能更加适合。

涉及到的数学公式

1. 初始化样本权重：
   $$w_i^{(1)} = \frac{1}{N} \quad \text{for} \quad i = 1, 2, \ldots, N$$

2. 弱分类器的权重计算：
   $$\epsilon_t = \sum_{i=1}^{N} w_i^{(t)} \cdot \mathbb{1}\left(h_t(x_i) \neq y_i\right)$$

   $$\alpha_t = \frac{1}{2} \ln\left(\frac{1 - \epsilon_t}{\epsilon_t}\right)$$

3. 样本权重更新：
   $$w_i^{(t+1)} = \frac{w_i^{(t)} \cdot \exp(-\alpha_t \cdot y_i \cdot h_t(x_i))}{Z_t} \quad \text{for} \quad i = 1, 2, \ldots, N$$

   其中，
   $$Z_t = \sum_{i=1}^{N} w_i^{(t)} \cdot \exp(-\alpha_t \cdot y_i \cdot h_t(x_i))$$

4. 最终分类器的组合：
   $$H(x) = \text{sign}\left(\sum_{t=1}^{T} \alpha_t \cdot h_t(x)\right)$$

这些公式涵盖了AdaBoost算法的核心数学原理。在这里，$N$ 表示样本数量，$x_i$ 是第 $i$ 个样本的特征，$y_i$ 是第 $i$ 个样本的标签，$h_t(x_i)$ 是第 $t$ 个弱分类器对样本 $x_i$ 的预测结果，$\alpha_t$ 是第 $t$ 个弱分类器的权重，$w_i^{(t)}$ 是第 $t$ 轮迭代中样本 $x_i$ 的权重，$T$ 是迭代轮数。

需要注意的是，这里的公式只是一个概览，实际的推导和计算过程可能会更加详细和复杂。如果你希望更深入地了解AdaBoost算法的数学原理，建议参考相关的教材、论文或在线资源。

案例：马疝病的预测

数据集

horseColicTest2.txt

/citation/AdaBoost/horseColicTest2.txt

horseColicTraining2.txt

/citation/AdaBoost/horseColicTraining2.txt

实现

import numpy as np

def load_sim_data():
    data_mat = np.matrix([[1.0, 2.1],
                          [2.0, 1.1],
                          [1.3, 1.0],
                          [1.0, 1.0],
                          [2.0, 1.0]])
    class_labels = [1.0, 1.0, -1.0, -1.0, 1.0]
    return data_mat, class_labels

def load_data_set(file_name):
    num_feat = len(open(file_name).readline().split('\t'))
    data_arr = []
    label_arr = []
    fr = open(file_name)
    for line in fr.readlines():
        line_arr = []
        cur_line = line.strip().split('\t')
        for i in range(num_feat - 1):
            line_arr.append(float(cur_line[i]))
        data_arr.append(line_arr)
        label_arr.append(float(cur_line[-1]))
    return np.matrix(data_arr), label_arr

def stump_classify(data_mat, dimen, thresh_val, thresh_ineq):
    ret_array = np.ones((np.shape(data_mat)[0], 1))
    if thresh_ineq == 'lt':
        ret_array[data_mat[:, dimen] <= thresh_val] = -1.0
    else:
        ret_array[data_mat[:, dimen] > thresh_val] = -1.0
    return ret_array

def build_stump(data_arr, class_labels, D):
    data_mat = np.mat(data_arr)
    label_mat = np.mat(class_labels).T
    m, n = np.shape(data_mat)
    num_steps = 10.0
    best_stump = {}
    best_class_est = np.mat(np.zeros((m, 1)))
    min_err = np.inf
    for i in range(n):
        range_min = data_mat[:, i].min()
        range_max = data_mat[:, i].max()
        step_size = (range_max - range_min) / num_steps
        for j in range(-1, int(num_steps) + 1):
            for inequal in ['lt', 'gt']:
                thresh_val = (range_min + float(j) * step_size)
                predicted_vals = stump_classify(data_mat, i, thresh_val, inequal)
                err_arr = np.mat(np.ones((m, 1)))
                err_arr[predicted_vals == label_mat] = 0
                weighted_err = D.T * err_arr
                if weighted_err < min_err:
                    min_err = weighted_err
                    best_class_est = predicted_vals.copy()
                    best_stump['dim'] = i
                    best_stump['thresh'] = thresh_val
                    best_stump['ineq'] = inequal
    return best_stump, min_err, best_class_est

def ada_boost_train_ds(data_arr, class_labels, num_it=40):
    weak_class_arr = []
    m = np.shape(data_arr)[0]
    D = np.mat(np.ones((m, 1)) / m)
    agg_class_est = np.mat(np.zeros((m, 1)))
    for i in range(num_it):
        best_stump, error, class_est = build_stump(data_arr, class_labels, D)
        alpha = float(0.5 * np.log((1.0 - error) / max(error, 1e-16)))
        best_stump['alpha'] = alpha
        weak_class_arr.append(best_stump)
        expon = np.multiply(-1 * alpha * np.mat(class_labels).T, class_est)
        D = np.multiply(D, np.exp(expon))
        D = D / D.sum()
        agg_class_est += alpha * class_est
        agg_errors = np.multiply(np.sign(agg_class_est) != np.mat(class_labels).T,
                                 np.ones((m, 1)))
        error_rate = agg_errors.sum() / m
        if error_rate == 0.0:
            break
    return weak_class_arr, agg_class_est

def ada_classify(data_to_class, classifier_arr):
    data_mat = np.mat(data_to_class)
    m = np.shape(data_mat)[0]
    agg_class_est = np.mat(np.zeros((m, 1)))
    for i in range(len(classifier_arr)):
        class_est = stump_classify(
            data_mat, classifier_arr[i]['dim'],
            classifier_arr[i]['thresh'],
            classifier_arr[i]['ineq']
        )
        agg_class_est += classifier_arr[i]['alpha'] * class_est
    return np.sign(agg_class_est)

def plot_roc(pred_strengths, class_labels):
    import matplotlib.pyplot as plt
    y_sum = 0.0
    num_pos_class = np.sum(np.array(class_labels) == 1.0)
    y_step = 1 / float(num_pos_class)
    x_step = 1 / float(len(class_labels) - num_pos_class)
    sorted_indicies = pred_strengths.argsort()
    fig = plt.figure()
    fig.clf()
    ax = plt.subplot(111)
    cur = (1.0, 1.0)
    for index in sorted_indicies.tolist()[0]:
        if class_labels[index] == 1.0:
            del_x = 0
            del_y = y_step
        else:
            del_x = x_step
            del_y = 0
            y_sum += cur[1]
        ax.plot([cur[0], cur[0] - del_x], [cur[1], cur[1] - del_y], c='b')
        cur = (cur[0] - del_x, cur[1] - del_y)
    ax.plot([0, 1], [0, 1], 'b--')
    plt.xlabel('False positive rate')
    plt.ylabel('True positive rate')
    plt.title('ROC curve for AdaBoost horse colic detection system')
    ax.axis([0, 1, 0, 1])
    plt.show()
    print("the Area Under the Curve is: ", y_sum * x_step)

def test():
    data_mat, class_labels = load_data_set('7.AdaBoost/horseColicTraining2.txt')
    weak_class_arr, agg_class_est = ada_boost_train_ds(data_mat, class_labels, 40)
    plot_roc(agg_class_est, class_labels)
    data_arr_test, label_arr_test = load_data_set("7.AdaBoost/horseColicTest2.txt")
    m = np.shape(data_arr_test)[0]
    predicting10 = ada_classify(data_arr_test, weak_class_arr)
    err_arr = np.mat(np.ones((m, 1)))
    print(m,
          err_arr[predicting10 != np.mat(label_arr_test).T].sum(),
          err_arr[predicting10 != np.mat(label_arr_test).T].sum() / m
          )

if __name__ == '__main__':
    test()

来源于 ApacheCN

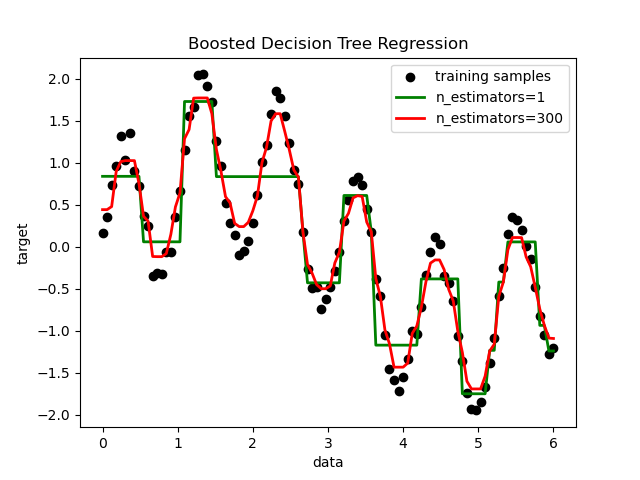
DT与AdaBoost

import matplotlib.pyplot as plt
import numpy as np
from sklearn import metrics
from sklearn.ensemble import AdaBoostRegressor
from sklearn.tree import DecisionTreeRegressor

rng = np.random.RandomState(1)
X = np.linspace(0, 6, 100)[:, np.newaxis]
y = np.sin(X).ravel() + np.sin(6 * X).ravel() + rng.normal(0, 0.1, X.shape[0])

regr_1 = DecisionTreeRegressor(max_depth=4)
regr_2 = AdaBoostRegressor(DecisionTreeRegressor(max_depth=4), n_estimators=300, random_state=rng)

regr_1.fit(X, y)
regr_2.fit(X, y)

y_1 = regr_1.predict(X)
y_2 = regr_2.predict(X)

plt.figure()
plt.scatter(X, y, c="k", label="training samples")
plt.plot(X, y_1, c="g", label="n_estimators=1", linewidth=2)
plt.plot(X, y_2, c="r", label="n_estimators=300", linewidth=2)
plt.xlabel("data")
plt.ylabel("target")
plt.title("Boosted Decision Tree Regression")
plt.legend()
plt.show()

print('y---', type(y[0]), len(y), y[:4])
print('y_1---', type(y_1[0]), len(y_1), y_1[:4])
print('y_2---', type(y_2[0]), len(y_2), y_2[:4])

y_true = np.array([0, 0, 1, 1])
y_scores = np.array([0.1, 0.4, 0.35, 0.8])
print('y_scores---', type(y_scores[0]), len(y_scores), y_scores)
print(metrics.roc_auc_score(y_true, y_scores))