期末复习-算法设计与分析

选择题

用贪心法解决背包问题时所用的贪心策略是(C)。
- A.重量小的物品优先装入背包
- B.价值大的物品优先装入背包
- C.单位重量的价值大的物品优先装入背包
- D.单位重量的价值小的物品优先装入背包
给定有序序列 T[]={1,4,6,8,10,12}，现在要用二分搜索算法查找指定元素 x=9 是否出现在序列 T 中，元素 x 要和序列元素比较(B)次能够得出结论。
- A.5
- B.3
- C.4
- D.2
0-1 背包问题：n=6，W=10，v(1:6)=(15,59,21,30,60,5)，w(1:6)=(1,5,2,3,6,1)。该问题的最大价值为(B)。
- A.101
- B.110
- C.115
- D.120
约束标准型线性规划问题的单纯形算法步骤，以下描述不正确的是(B)。
- A.找出基本变量和非基本变量
- B.判断检验数 C 是否为整数，如果是，算法无界结束
- C.选入基变量
- D.选离基变量
某算法的计算时间 T(n)满足递归关系式：T(n)=2T(n/2)+1，n>1；T(1)=1。则Ｔ(n)=(C)。
- A.$n\log{n}$
- B.$\log{n}$
- C.$n$
- D.$n\lg{n}$
随机快速排序算法中，选取基准元素的方法是(D)。
- A.选序列的第一个元素作为基准元素
- B.选序列的最后一个元素作为基准元素
- C.选序列的中间位置的元素作为基准元素
- D.随机选择序列中的一个元素作为基准元素
将一般线性规划转化为标准线性规划的过程中，以下描述不正确的是(B)。
- A.将最小化目标转化成最大化目标时，需要将目标函数两边同乘以（-1）
- B.将小于等于的约束转化为等于约束时，需要在小的一方添加一个大于 0 的松弛变量
- C.将大于等于的约束转化为等于约束时，需要在大的一方去掉一个大于等于 0 的人工变量
- D.将小于等于的约束转化为等于约束时，需要在小的一方添加一个大于等于 0 的人工变量
最长公共子序列问题中，给定两个序列的长度分别为 m、n，求这两个序列的最长公共子序需要耗时(D)。
- A.$O(m^2)$
- B.$O(n^2)$
- C.$O(m^n)$
- D.$O(mn)$
分治法中，将规模大的问题分解为多个子问题，子问题必须满足的条件是(BCD)。
- A.一般不相互独立
- B.相互独立
- C.规模变小
- D.与原问题相同
有关 Kruskal 算法的描述说法正确的是(A)。
- A.Kruskal 算法的时间复杂度为($e\log{e}$)，其中 e 为无向连通图的边数
- B.对稠密图，Kruskal 算法比 Prim 算法有效
- C.对稀疏图，Kruskal 算法比 Prim 算法有效
- D.对任何无向连通图，Kruskal 算法都比 Prim 算法有效
某算法的时间复杂度表达式为$T(n) = 30n^4+20n^3+40n^2+46n+100$，该算法的时间复杂度可以用下列哪个渐进意义下的符号表示(A)。
- A.$O$
- B.$\Omega$
- C.$\Theta$
- D.以上符号都不能用来表示
二分查找的时间复杂度为(C)。
- A.$O(n\log{n})$
- B.$O{n}$
- C.$O(\log{n})$
- D.以上都不对
最长公共子序列问题中，给定两个序列 X={A,B,C,B,D,A,B}和 Y={A,C,B,E,D,B}，这两个序列的最长公共子序的长度为(C)。
- A.3
- B.6
- C.5
- D.4
矩阵连乘问题：M1(5×10), M2(10×4), M3(4×6)。矩阵链乘 M1M2M3 需要的最少的乘法次数为(B)。
- A.540
- B.320
- C.720
- D.300
用贪心法设计算法的关键是(B)。
- A.将问题分解为多个子问题来分别处理
- B.选好贪心策略
- C.获取各阶段间的递推关系式
- D.满足最优性原理
矩阵连乘积问题：M1(5×10), M2(10×4), M3(4×6)。矩阵链乘 M1M2M3 需要的最少乘法次数为(D)。
- A.348
- B.328
- C.720
- D.320
下列(A)不是描述算法的工具。
- A.数据流图
- B.伪代码
- C.自然语言
- D.程序语言
算法必须满足的特性除了有能行性和确定性外，还有(B)。
- A.输出
- B.有限性
- C.输入
- D.无限性
分支限界法与回溯法的不同主要表现，以下错误的是(C)。
- A.搜索目标
- B.搜索方式
- C.搜索开始
- D.扩展方式
算法具有的五种特性分别是输入、输出、(C)、有限性、可行性。
- A.鲁棒性
- B.二义性
- C.确定性
- D.兼容性
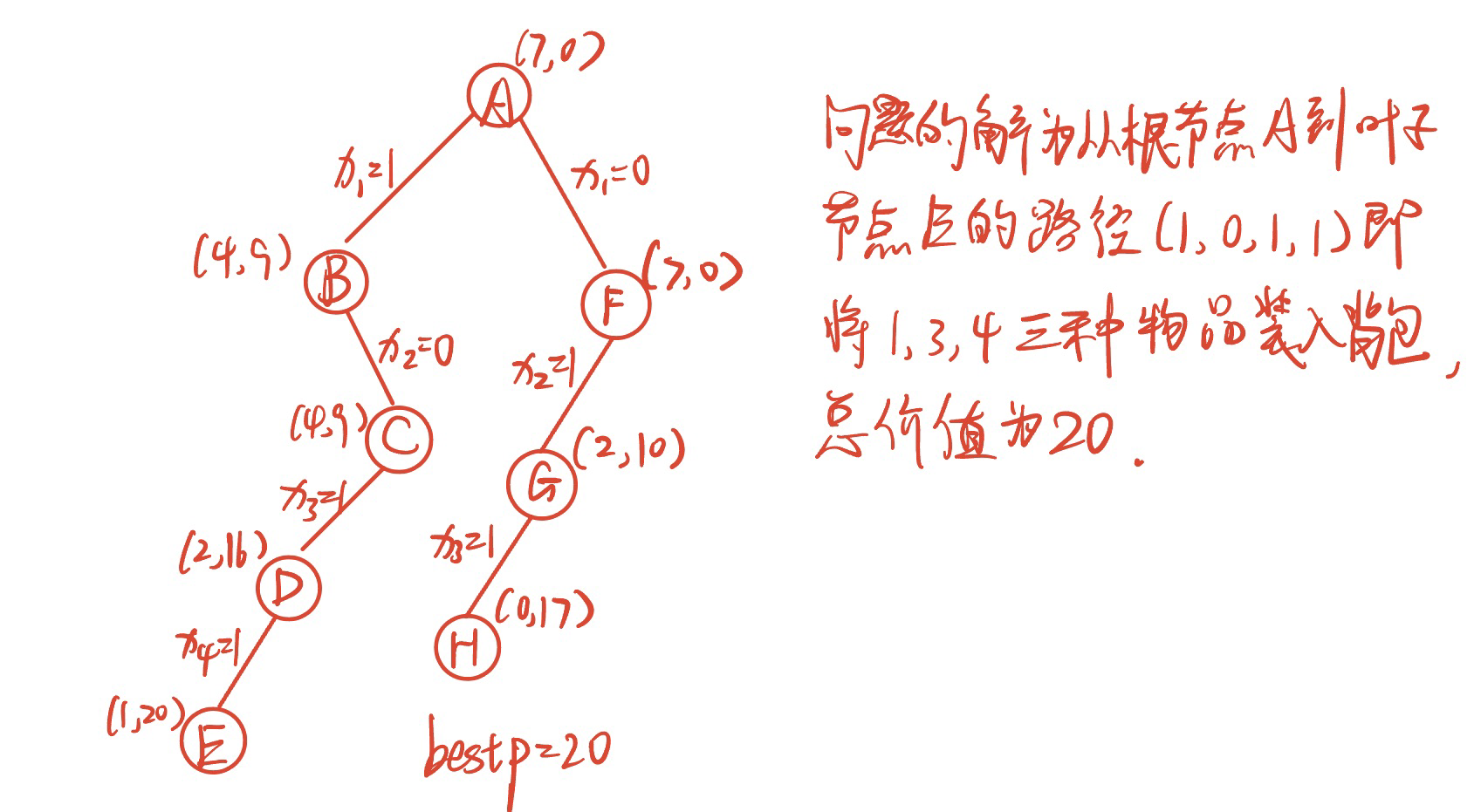
背包问题：给定$n=4 \quad W=7 \quad w=(3,5,2,1) \quad p=(9,10,7,4)$，该问题的最大价值是(B)。
- A.19
- B.20
- C.21
- D.22

填空题

算法复杂性是指算法在计算机上运行时所消耗的计算机资源的量。最重要的计算机资源是(时间资源)和(空间资源)
回溯法算法框架中定义问题的解空间时，解的形式是($ \left( x_1, x_2, \dots, x_n \right) $ )；解空间结构的组织形式通常有(子集数)、(排列树)、(满m叉树)。
分支限界法中，从活结点表中选择下一个扩展结点的不同方式导致了不同的分支限界法，最常见的有(对列式分支限界法)和(优先队列式分支限界法)。
贪心法的两个基本要素是(最优子结构性质)和(贪心选择性质)。
分治法的求解分为(分解)和(治理)两大步骤。
最大团问题的解空间树是(子集)树，旅行商问题的解空间树是(排列)树。

用分治法设计的合并排序算法描述如下，其中A[low:high]存放的待排序序列，请填写空缺部分的语句。

void MergeSort(int A[], int low, int high) {
    int middle;
    if (low < high) {
        // please input: middle = (low + high) / 2;
        MergeSort(A, low, middle); // 递归排序左半部分
        // please input: MergeSort(A, middle + 1, high);
        Merge(A, low, middle, high); // 合并两个有序子序列
    }
}

使用算法 LCS 找两个序列 A=”xzyzzyx”和 B=”zxyyzxz”的最长的公共子序列。它的一个最长公共子序列为(xyzz)，长度是(4)。
某算法的计算时间$ T(n) $满足递归关系式：$ T(n)=2T(n-1)+O(1) \quad n>1 \And T(1)=1 $。则$ T(n) $ = ($ O(2^n) $)。
活动安排问题的贪心策略是(时间结束早的优先安排)。
矩阵连乘问题算法借助于(二维数组)存放各子问题的最优值。

用分治法设计的快速排序算法描述如下，其中R[low:high]存放的待排序序列，请填写空缺部分的语句。

void QuickSort(int R[], int low, int high) {
    int pivotpos; // 记录基准元素所在位置
    if (low < high) {
        pivotpos = Partition(R, low, high);
        // please input: QuickSort(R, low, pivotpos - 1);
        QuickSort(R, pivotpos+1, high);
    }
}

求解题

采用合并排序的思想将给定序列 T[1:9]={5,3,8,2,1,9,23,12,6} 由小到大排序。(要求：只写出首次分解得到两个子问题的过程、递归的结果、子问题的解合并成原问题的解的过程)
1. $\frac{\left( 1+9 \right)}{2}=5$
2. 两个子问题分别为：$T[1:5]= { 5,3,8,2,1} \quad T[6:9]= {9,23,12,6}$
3. 递归求解：$T[1:5]= {1,2,3,5,8} \quad T[6:9]= {6,9,12,23}$
4. 将两个问题的解合并为原问题的解
  1. 根据合并的算法$[1,2,3,5]$放入辅助数组中
  2. 将$[6]$放入辅助数组中
  3. 将$[8]$放入辅助数组中
  4. 将$[9,12,23]$放入辅助数组中
  5. 将辅助数组复制到原数组中，得到原问题的解$T[1:9]={1,2,3,5,6,8,9,12,23}$
请用 Prim 算法求解如下图所示的最小生成树（要求：写出生成最小生成树的过程）
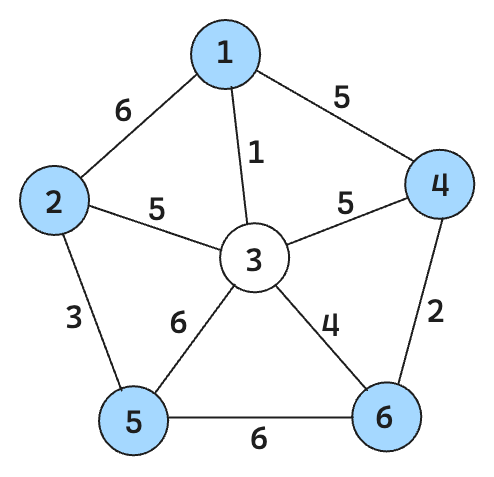
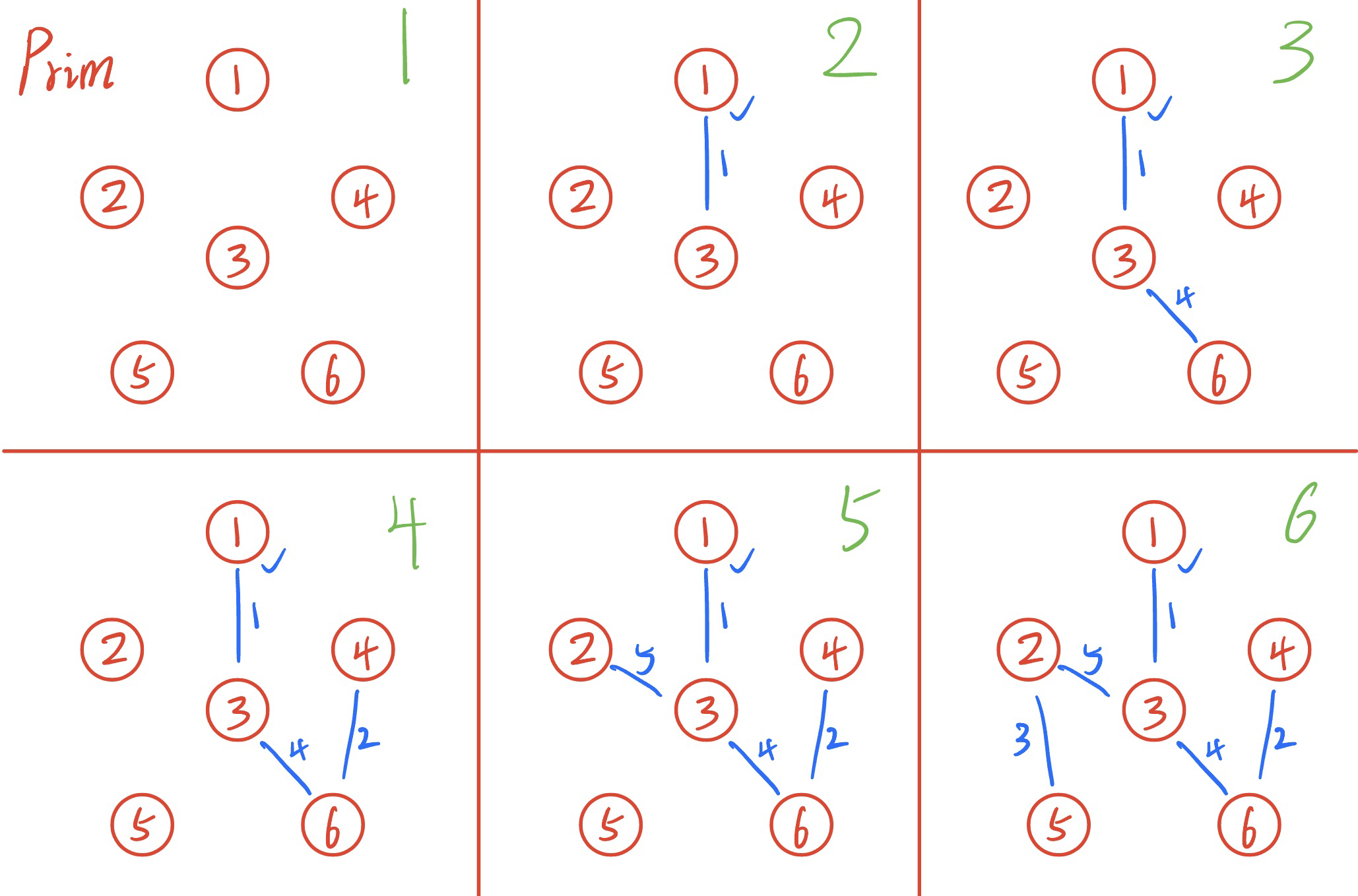
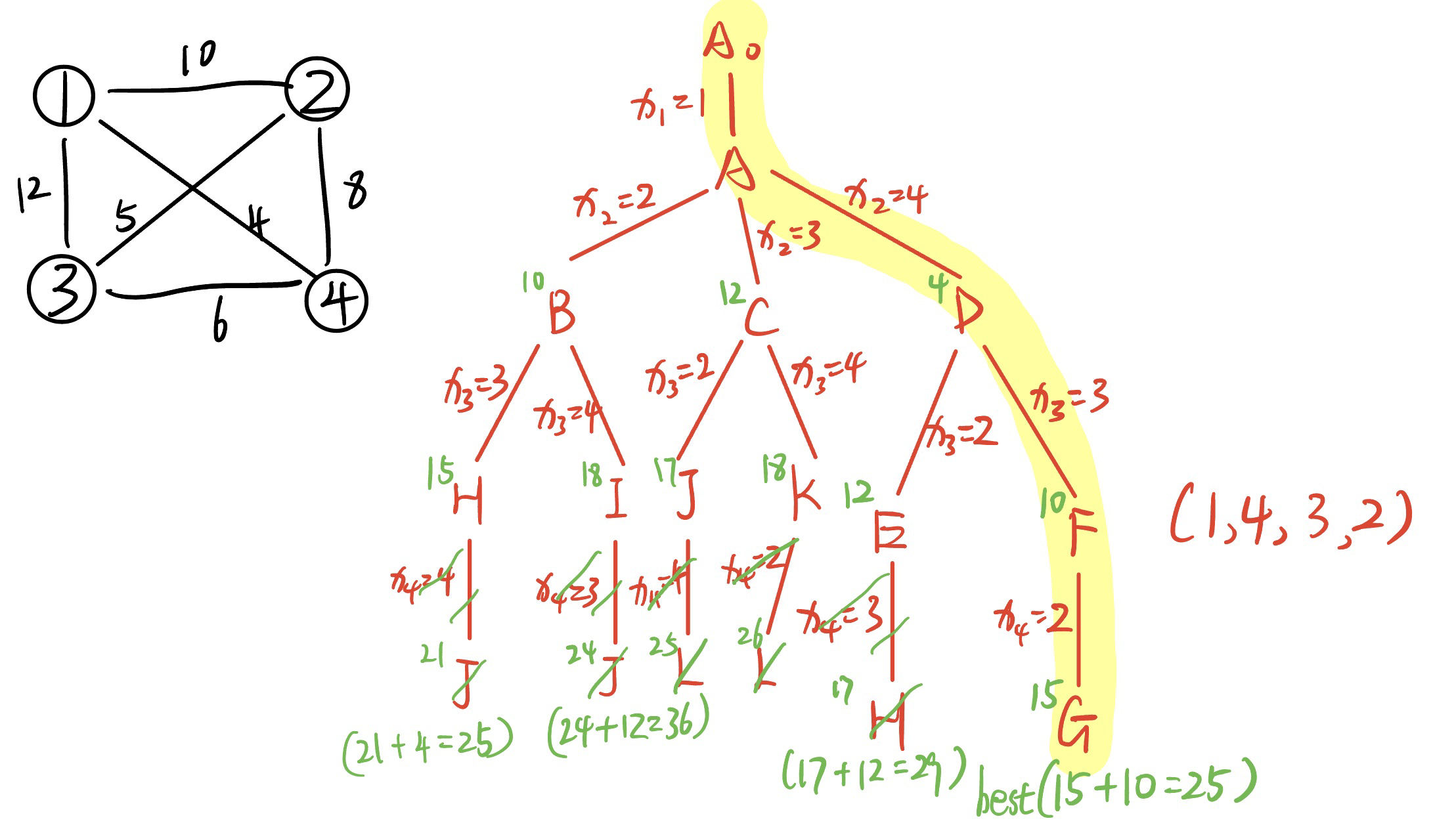
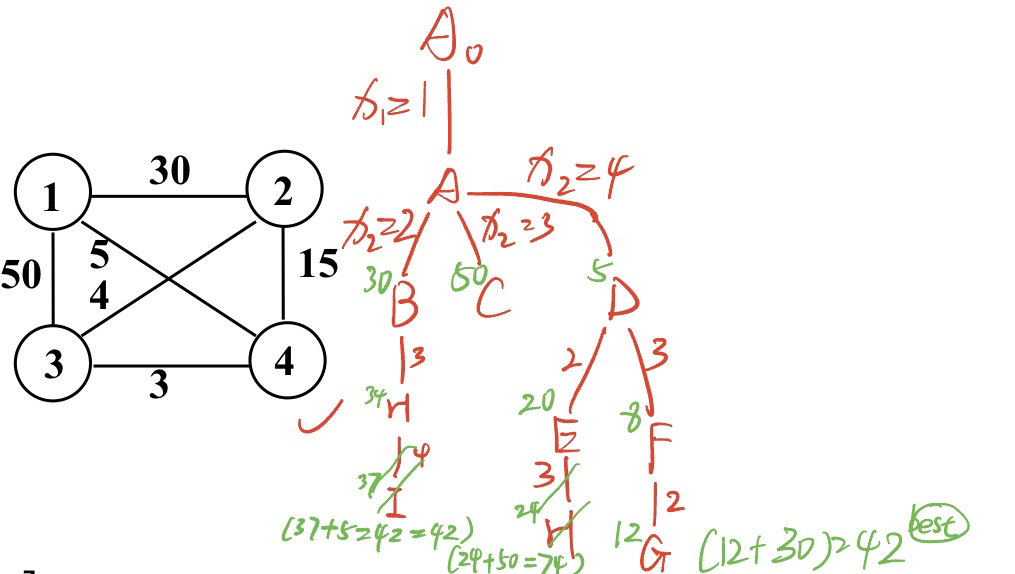
用优先队列式分支限界法解如下旅行售货员问题。假设当前旅行售货员的住地为 1 号城市，边上的权为城市之间的交通费用，要求从 1 号城市出发，到其它城市各去一次推销商品，然后再回到住地所花费的总交通费用最少的路线。（要求：做好搜索前的准备，然后用搜索树展示搜索过程）
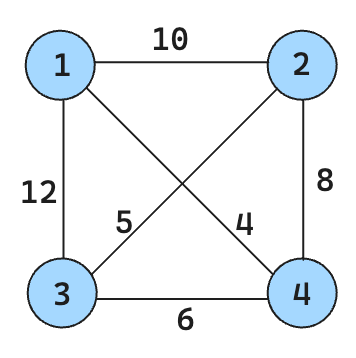
用单纯性算法求解下面线性规划问题：
$$\max{z} = -x_2 + 3x_3 - 2x_4$$

Subject to:
- $ x_1 + 3x_2 - x_3 + 2x_4 = 7 $
- $ -4x_2 + 3x_3 + 8x_4 \leq 10 $
- $ 2x_2 - 4x_3 \geq -12 $
- $ x_i \geq 0 (i=1,2,3,4) $
要求
1. 步骤描述
2. 写清每一迭代步的选择，单纯形表，可行解及可行解对应的目标函数的值。
解：
1. 标准化->单纯型表->转轴旋转->直到检验数$\le 0$
2. 标准化
  $$ \max z=x_2+3x_3-2x_4 $$
  $$ x_1+3x_2-x_3+2x_4=7 $$
  $$ -4x_2+3x_3+8x_4+x_5=10 $$
  $$ -2x_2+4x_3+x_6=12 $$
  $$x_i \ge 0 \quad (i=1,2,3,4,5,6) $$
3. 单纯型表
4. $x_2$ $x_3$ $x_4$ $b$
  
  $z$ 1 3 -2 0
  
  $x_1$ 3 -1 2 7
  
  $x_5$ -4 3 8 10
  
  $x_6$ -2 4 0 12
  
  可行解：$X^{0}=(7,0,0,0,10,12) \quad z=0$，入基变量为$x_3$，离基变量为$x_6$
5. 单纯型表
  
  $x_2$ $x_6$ $x_4$ $b$
  
  $z$ 5/2 -3/4 -2 9
  
  $x_1$ 5/2 1/4 2 10
  
  $x_5$ -5/2 -3/4 8 1
  
  $x_3$ -1/2 1/4 0 3
6. 可行解：$X^1=(10,0,3,0,1,0) \quad z=9$，入基变量为$x_2$，离基变量为$x_1$
7. 单纯型表
  
  $x_1$ $x_6$ $x_4$ $b$
  
  $z$ -1 -1 -4 19
  
  $x_2$ 2/5 1/10 4/5 4
  
  $x_5$ 1 1/2 10 11
  
  $x_3$ -1/5 3/10 2/5 5
8. 可行解：$X^2=(0,4,5,0,11,0) \quad z=19$
9. 以上线性规划最优解为：$X^2=(0,4,5,0,11,0)$，最优值为：$z=19$
用单纯性算法求解下面约束标准型线性规划问题：
$$\min{z}=x_2-3x_3+2x_4$$

Subject to:
- $ -2x_2 + 4x_3 + x_5 = 12 $
- $ -4x_2 + 3x_3 + 8x_4 \leq 10 $
- $ x_1 + 3x_2 - x_3 + 2x_4 = 7 $
- $ x_i \geq 0 (i=1,2,3,4,5) $
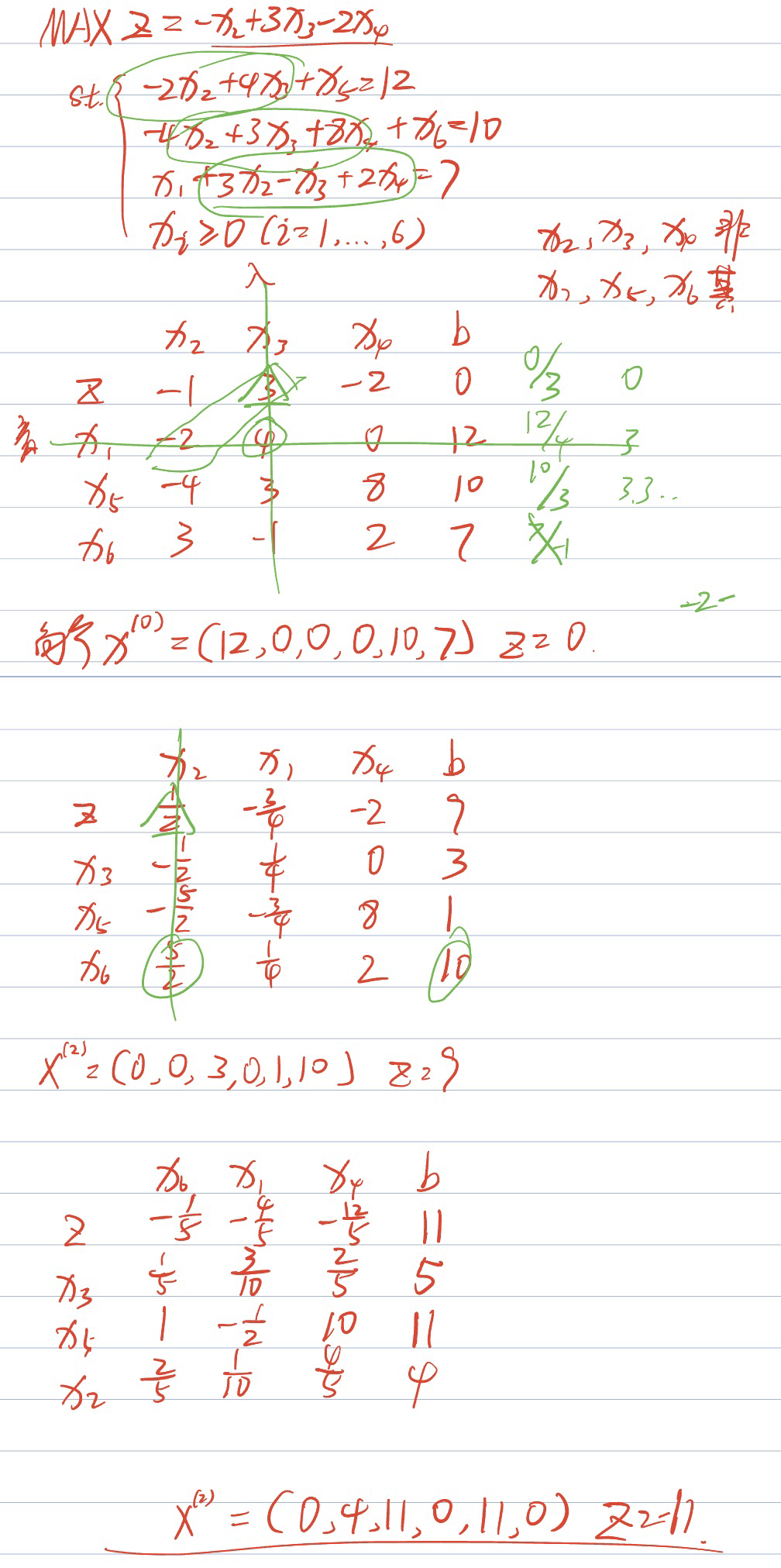
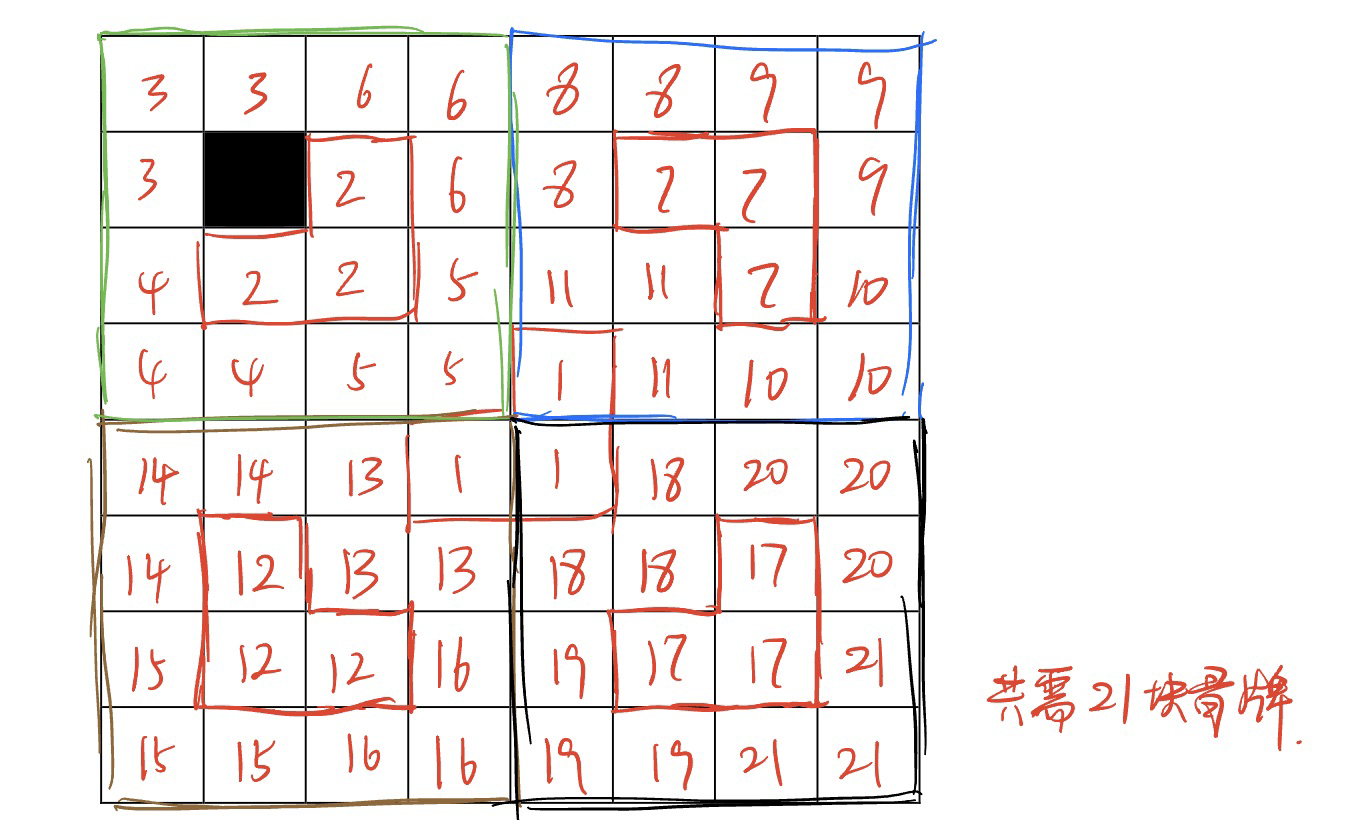
按分治策略求解棋盘覆盖问题时，对于如下图所示的 k=3 的特殊棋盘，共需要多少个 L 型骨牌；并在棋盘上填写 L 型骨牌的覆盖情况。
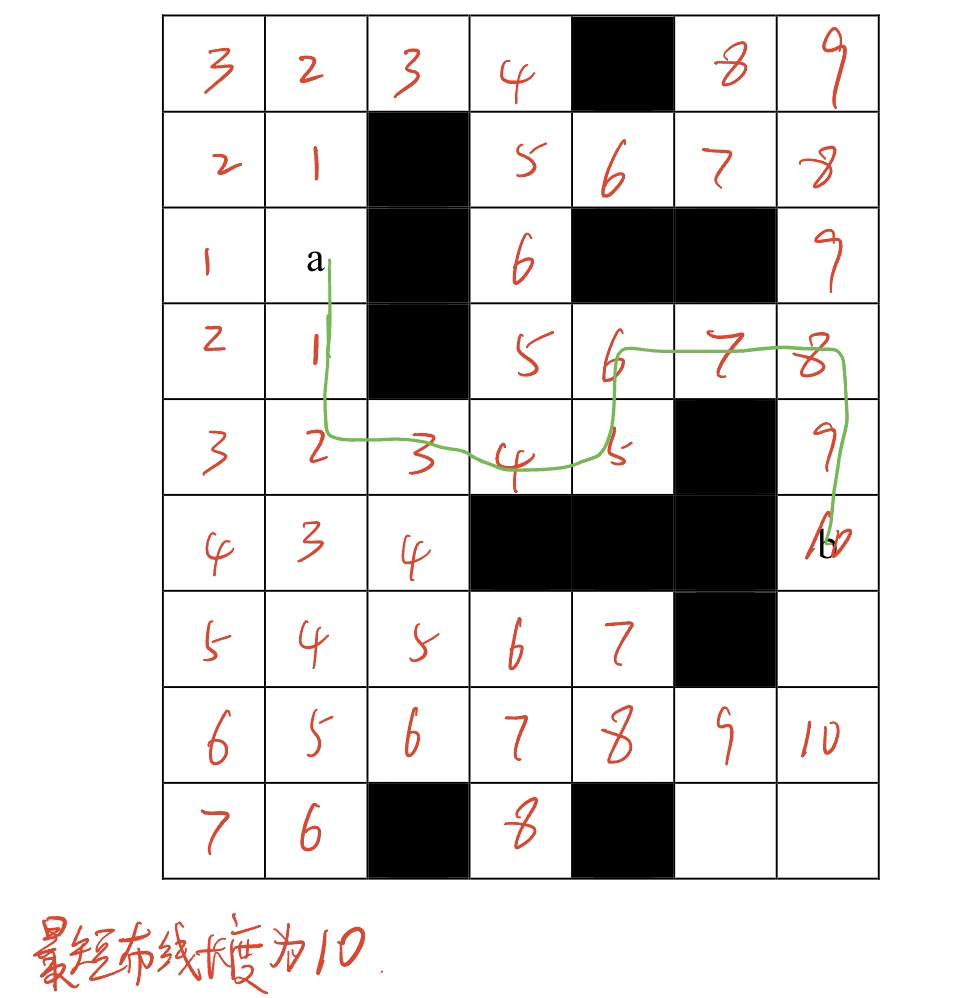
已知在如下所示的电路板中，阴影部分是已作了封锁标记的方格，请按照队列式分支限界法在图中确定 a 到 b 的最短布线方案，要求布线时只能沿直线或直角进行，在图中标出求得最优解时各方格情况。
用动态规划法求最优加工顺序问题：有 7 个工件在第一台机器和第二台机器上的处理时间分别为[3，8，10，12，6，9，15]，[7，2，6，18，3，10，4]。（要求：先按求解步骤分为两个序列，然后对序列排序合并，再写具体的求解过程，指出最优解）

解：
1. 令$N_1={i \mid a_i \lt b_i }={1,4,6} \quad N_2={i \mid a_i \ge b_i }={2,3,5,7}$
2. $N_1={i \mid a_i \lt b_i }={1,6,4} \quad N_2={i \mid a_i \ge b_i }={3,7,5,2}$
3. $N_1,N_2={1,6,4,3,7,5,2}$
对于矩阵$[2,3],[3,5],[5,9],[9,10]$的连乘问题，找到它的最优值和最优解，用数学表示出来。
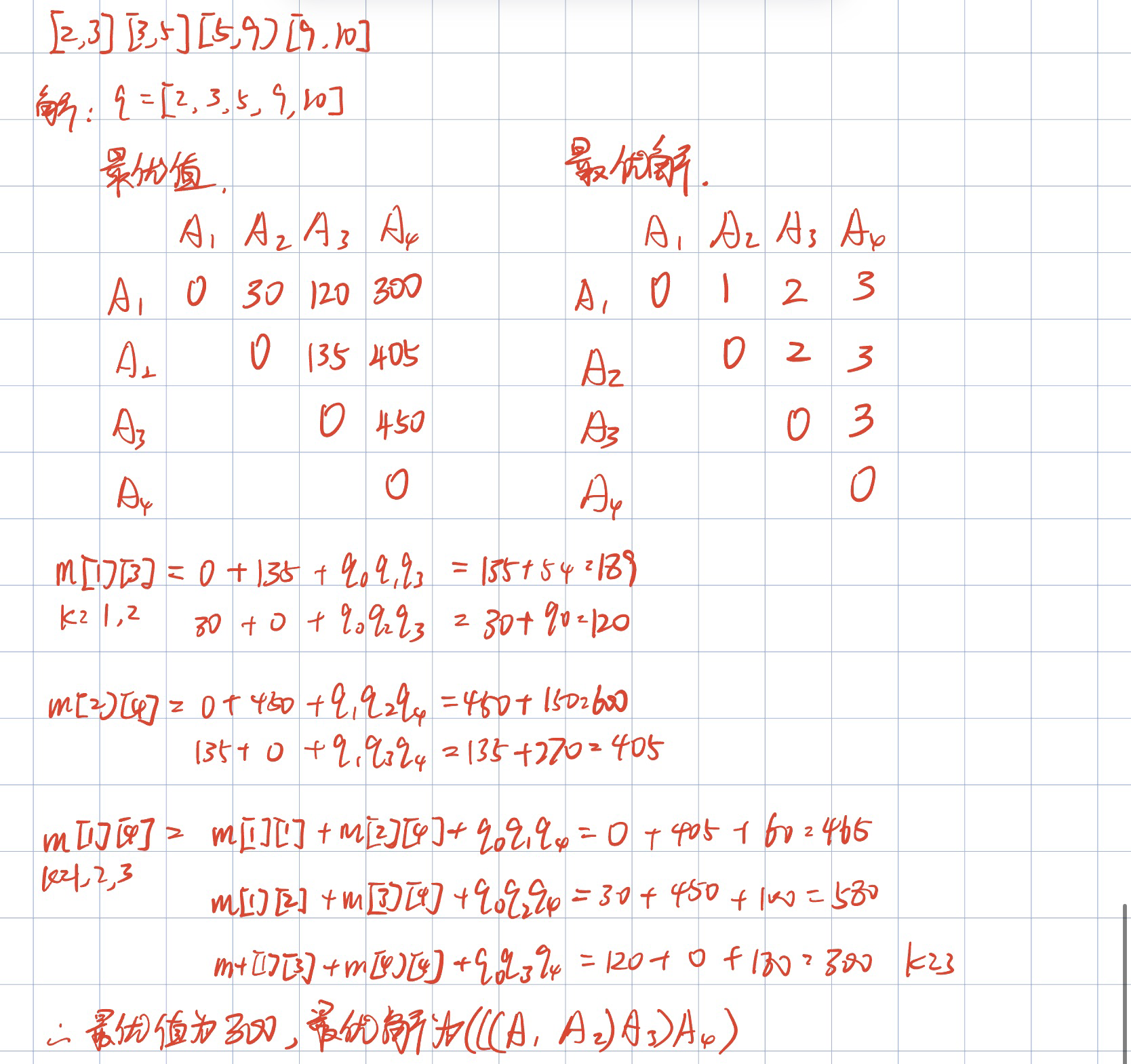
对于矩阵$[3,2],[2,5],[5,10],[10,2]$的连乘问题，找到它的最优值和最优解，用数学表示出来。
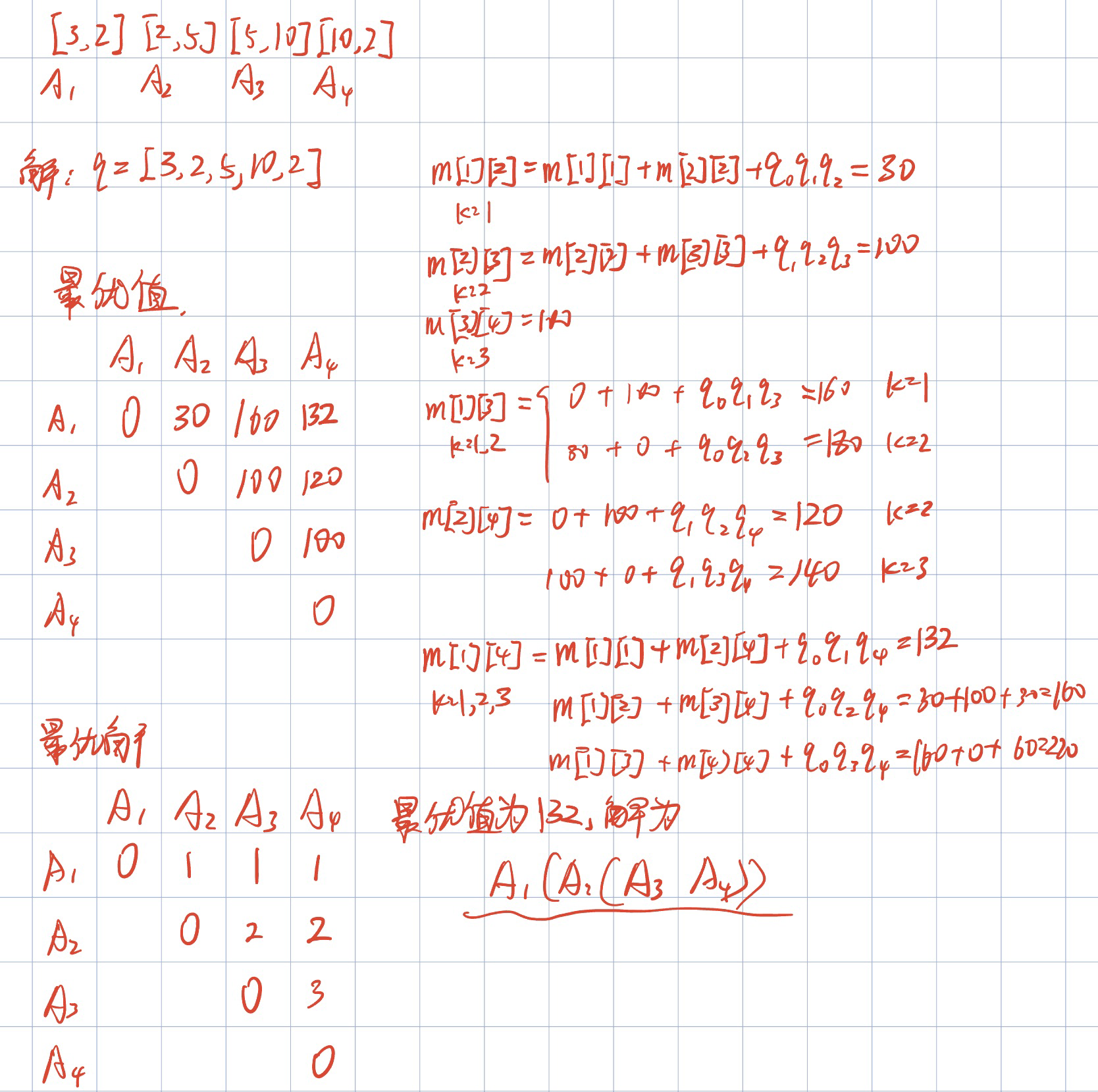
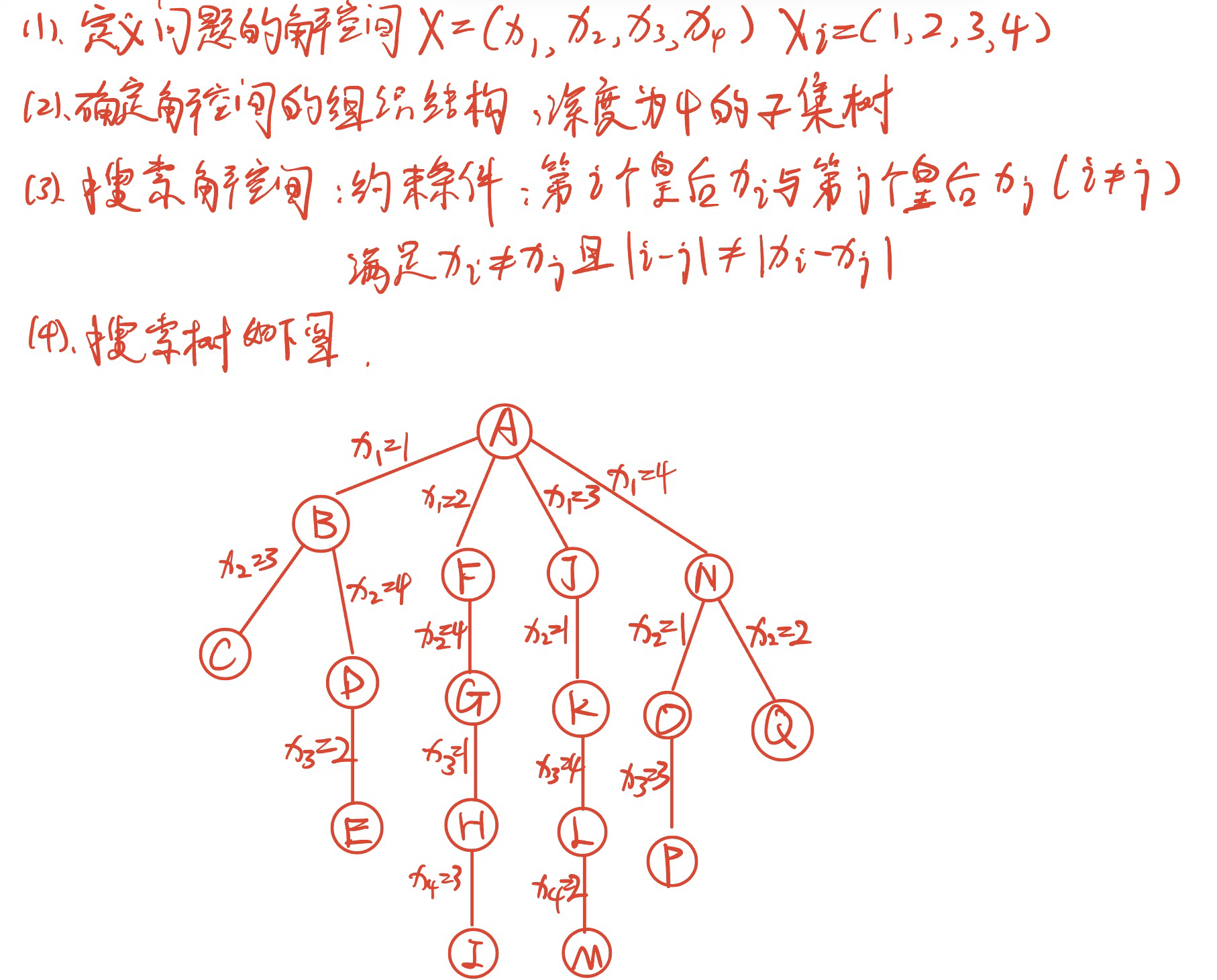
用分支限界法解决解 4 皇后问题。(请写出解题思想及求解步骤)
用分支限界法解决 0-1 背包问题:重量 w=[3，5，2，1]，价值 v=[9，10，7，4]，最大容量 C=7。(请写出解题思想及求解步骤)