期末复习-应用统计学

部分问题答案无法在高亮内显示，于是使用==来将内容标注

填空题

$T^2$分布与$F$分布的关系为：若$T^2 \sim T^2 \left( p,n \right)$则$\frac{n-p+1}{np} T^2 \sim F$(==p,n-p+1==)
设$X_{(1)}, \dots ,X_{(n)}$是来自正态总体$X \sim N_p \left( \mu,\Sigma \right)$的随机样本，但$\Sigma = \Sigma_0$已知时进行单总体均值向量的假设检验，$\bar{X} \sim N_p \left( \mu,\frac{\Sigma_0}{n} \right) \quad \sqrt{n}\left(\bar{X}-\mu \right) \sim N_p \left(0,\Sigma_0\right) $，则当$H_0$成立时，统计量$T^2 = n \cdot (\bar{X} - \mu_0)^T \Sigma^{-1} (\bar{X} - \mu_0) \sim $==$\chi^2(p)$==
因子分析中，因子载荷量的统计意义是利用标准化的的数据计算的相关阵$R$的特征值所对应的特征向量。
常用的判别方法有距离判别、贝叶斯判别、费希尔判别。
设$A$是载荷矩阵，则衡量（公共）因子重要性的一个量是A 中列元素的平方和。
设$x, y$是从均值向量分别是$\mu$，协方差阵时$\Sigma$的总体中抽取的两个样本，则$x$与$y$之间的马氏距离$d_{(x, y)} = $==$\sqrt{(x-y)’\Sigma^{-1}(x-y)}$==。
在 R 语言中散点图调用的函数为plot。
设$X \sim N_p(\mu, \Sigma)$，$B$为$s \times p$的常数矩阵，$d$为$s$维常数向量，令$Y = BX + d$，则$Y \sim$==$N_s(B \mu + d, B \Sigma B’)$==。
设$X \sim N_2(\mu, \Sigma)$，其中$X = (x_1, x_2) \quad \mu = (\mu_1, \mu_2) \quad \Sigma = \sigma^2 \begin{bmatrix} 1 & \rho \\ \rho & 1 \end{bmatrix}$，则$x_1 + x_2$与$x_1 - x_2$独立。
P 个随机变量的总方差为协方差矩阵$\Sigma$的特征值之和。
样本主成分的总方差与原变量样本的总方差相等。

判断题

对于两组的判别，最大后验概率法判别规则可使两个误判概率之和达到最小。$\times$
$R$型聚类分析的分类对象是样品。$\times$
在聚类分析中使用主成分的目的是为了更好地计算样品间的距离。$\times$
在正交因子模型中，因子载荷完全决定了原始变量之间的协方差或相关系数。$\checkmark$
对应分析图中行点和列点之间的距离是没有意义的。$\times$
费希尔判别既可用于分类也可用于分离，且在实际应用中更多地用于分离。$\checkmark$
马氏距离不受变量单位的影响。$\checkmark$
正交旋转将改变共性方差。$\times$
对应分析图中相近的行点和列点之间的关联性与它们离原点的远近无关。$\times$
主成分之间互不相关，它们的方向彼此垂直。$\checkmark$

计算题

设$X \sim N_3 \left( \mu,2I_3 \right)$，已知$\mu = \begin{bmatrix} 2 \\ 0 \\ 0 \end{bmatrix} \quad A = \begin{bmatrix} 0.5 & -1 & 0.5 \\ -0.5 & 0 & -0.5 \end{bmatrix} \quad d = \begin{bmatrix} 1 \\ 2 \end{bmatrix}$试求$Y = AX + d$的分布。
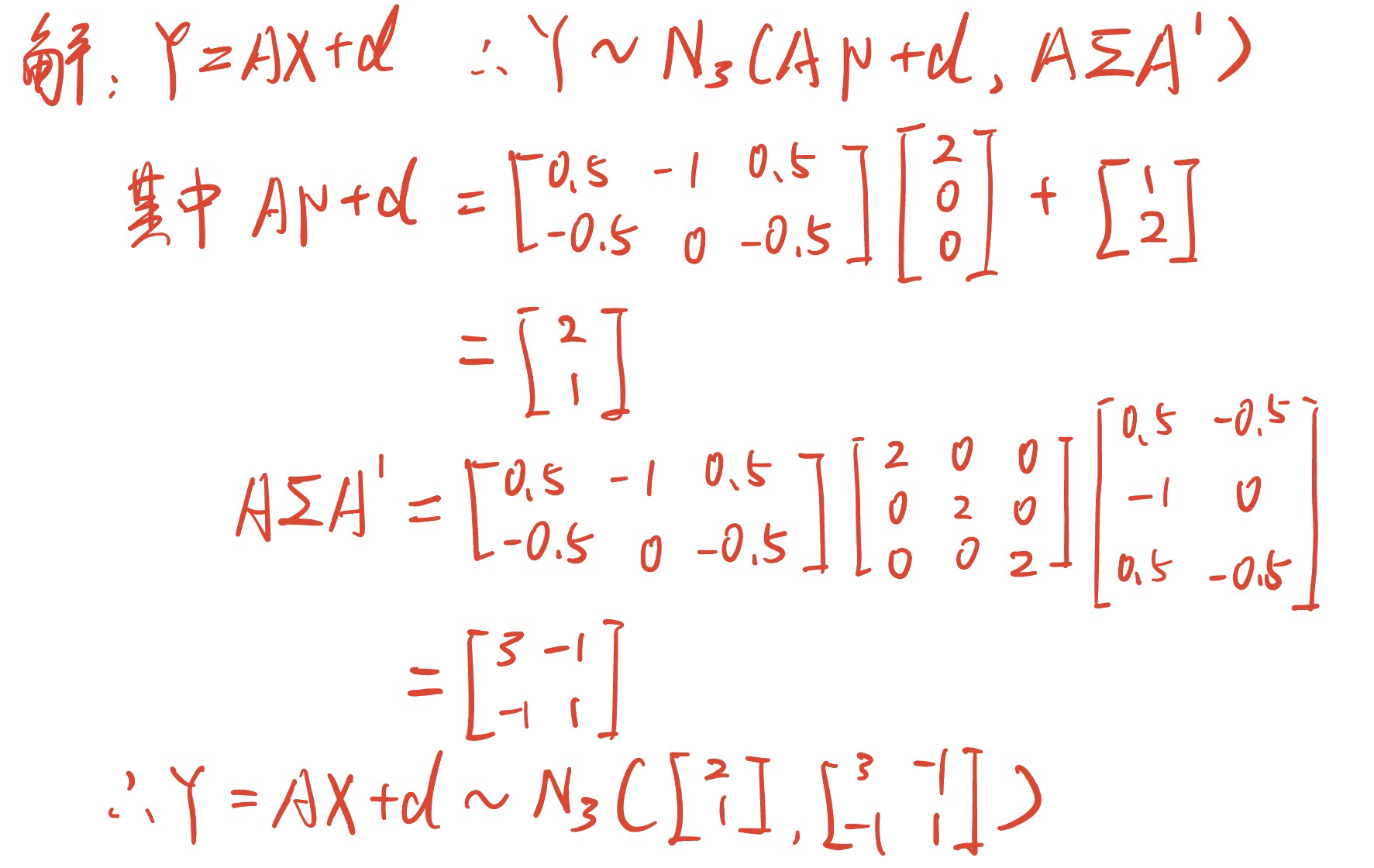
设$X = \left( x_1,x_2,x_3 \right)’ \sim N_3(\mu,\Sigma)$，其中$\mu = \begin{bmatrix} 2 \\ -3 \\ 1 \end{bmatrix} \quad \Sigma = \begin{bmatrix} 1 & 1 &1 \\ 1 & 3 & 2 \\ 1 & 2 & 2 \end{bmatrix}$。

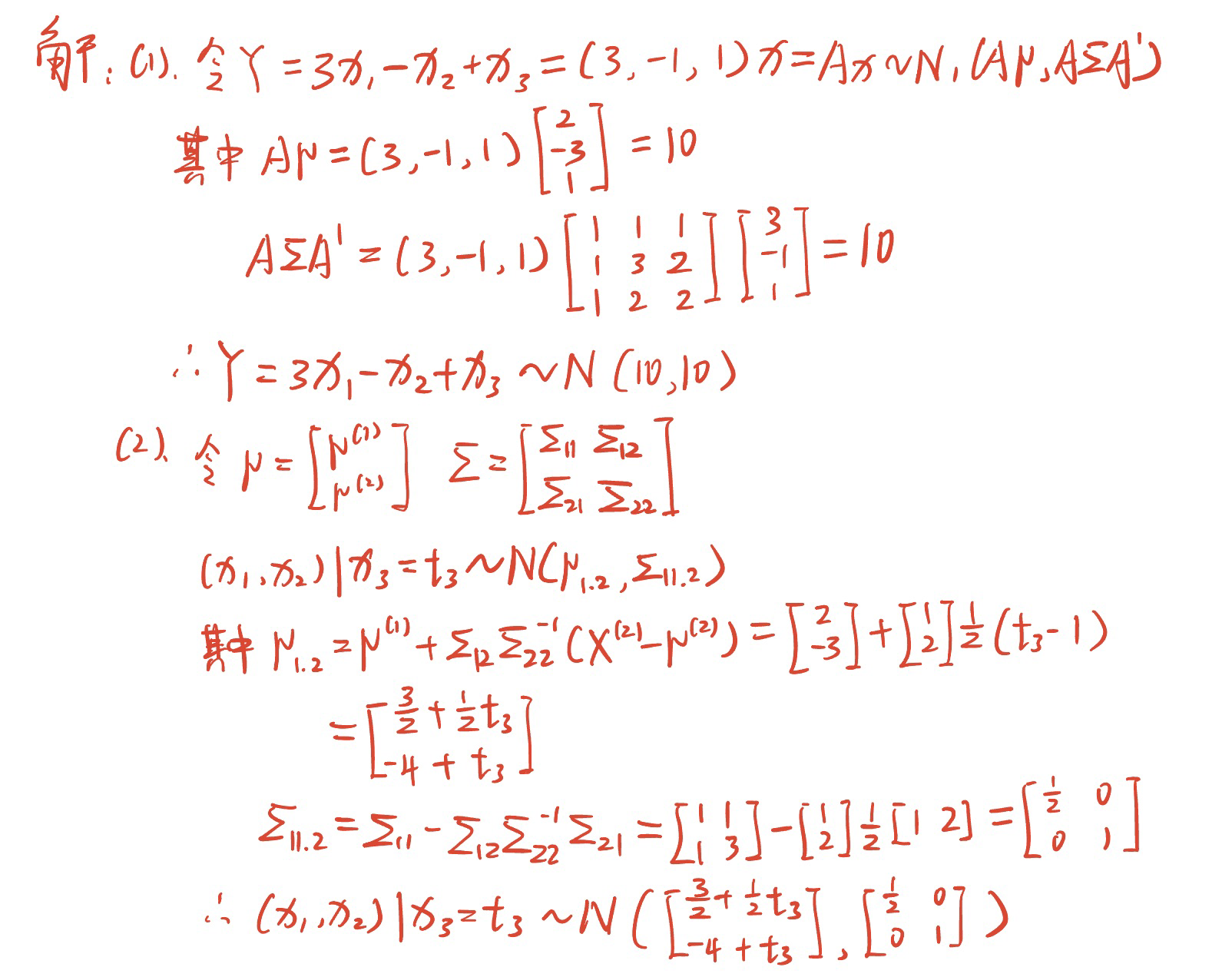
试检验假设$H_0 : \mu = \mu_0 \leftrightarrow H_1 : \mu \neq \mu_0 \left( \alpha=0.05 \right)$
设误判损失、先验概率及目睹概率值如下图

	$G_1$	$G_2$	$G_3$
$G_1$	$L\left( 1 \lvert 1 = 0 \right)$	$L\left( 2 \lvert 1 = 10 \right)$	$L\left( 3 \lvert 1 = 200 \right)$
$G_2$	$L\left( 1 \lvert 2 = 20 \right)$	$L\left( 2 \lvert 2 = 0 \right)$	$L\left( 3 \lvert 2 = 100 \right)$
$G_3$	$L\left( 1 \lvert 3 = 60 \right)$	$L\left( 2 \lvert 3 = 50 \right)$	$L\left( 3 \lvert 3 = 0 \right)$
先验概率	$p_1 = 0.05$	$p_2 = 0.65$	$p_3 = 0.3$
概率密度	$f_1 \left( x_0 \right) = 0.1$	$f_2 \left( x_0 \right) = 0.63$	$f_3 \left( x_0 \right) = 2.4$

试根据最小 ECM 判别准则判断$x_0$应归属于哪一个总体。

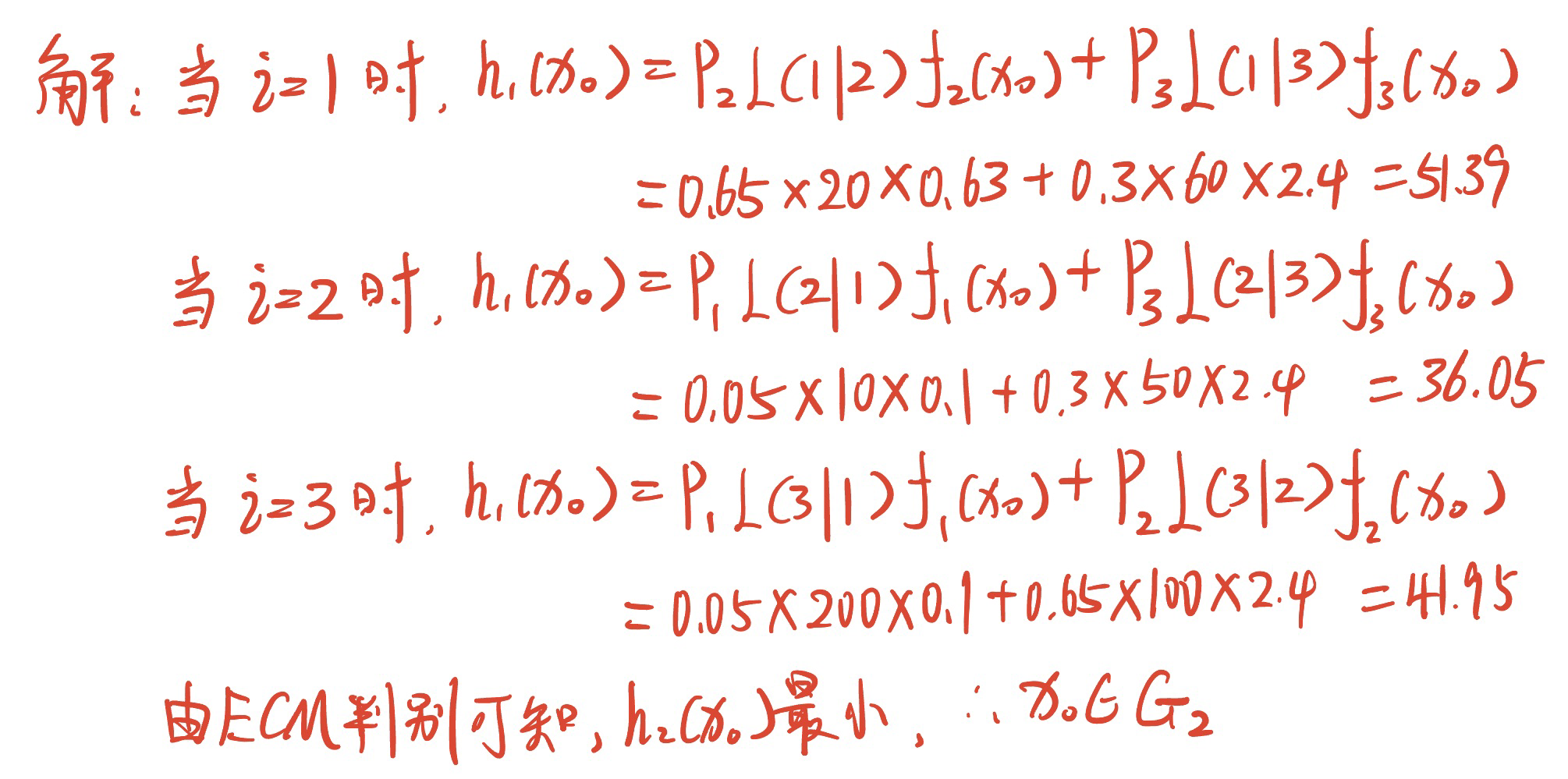
试检验假设$H_0 : \mu = \mu_0 \leftrightarrow H_1 : \mu \neq \mu_0 \left( \alpha=0.05 \right)$
设误判损失、先验概率及目睹概率值如下图

	$G_1$	$G_2$	$G_3$
$G_1$	$L\left( 1 \lvert 1 = 0 \right)$	$L\left( 2 \lvert 1 = 30 \right)$	$L\left( 3 \lvert 1 = 60 \right)$
$G_2$	$L\left( 1 \lvert 2 = 350 \right)$	$L\left( 2 \lvert 2 = 0 \right)$	$L\left( 3 \lvert 2 = 200 \right)$
$G_3$	$L\left( 1 \lvert 3 = 120 \right)$	$L\left( 2 \lvert 3 = 70 \right)$	$L\left( 3 \lvert 3 = 0 \right)$
先验概率	$p_1 = 0.5$	$p_2 = 0.2$	$p_3 = 0.3$
概率密度	$f_1 \left( x_0 \right) = 0.36$	$f_2 \left( x_0 \right) = 0.12$	$f_3 \left( x_0 \right) = 0.67$

试根据最小 ECM 判别准则判断$x_0$应归属于哪一个总体。

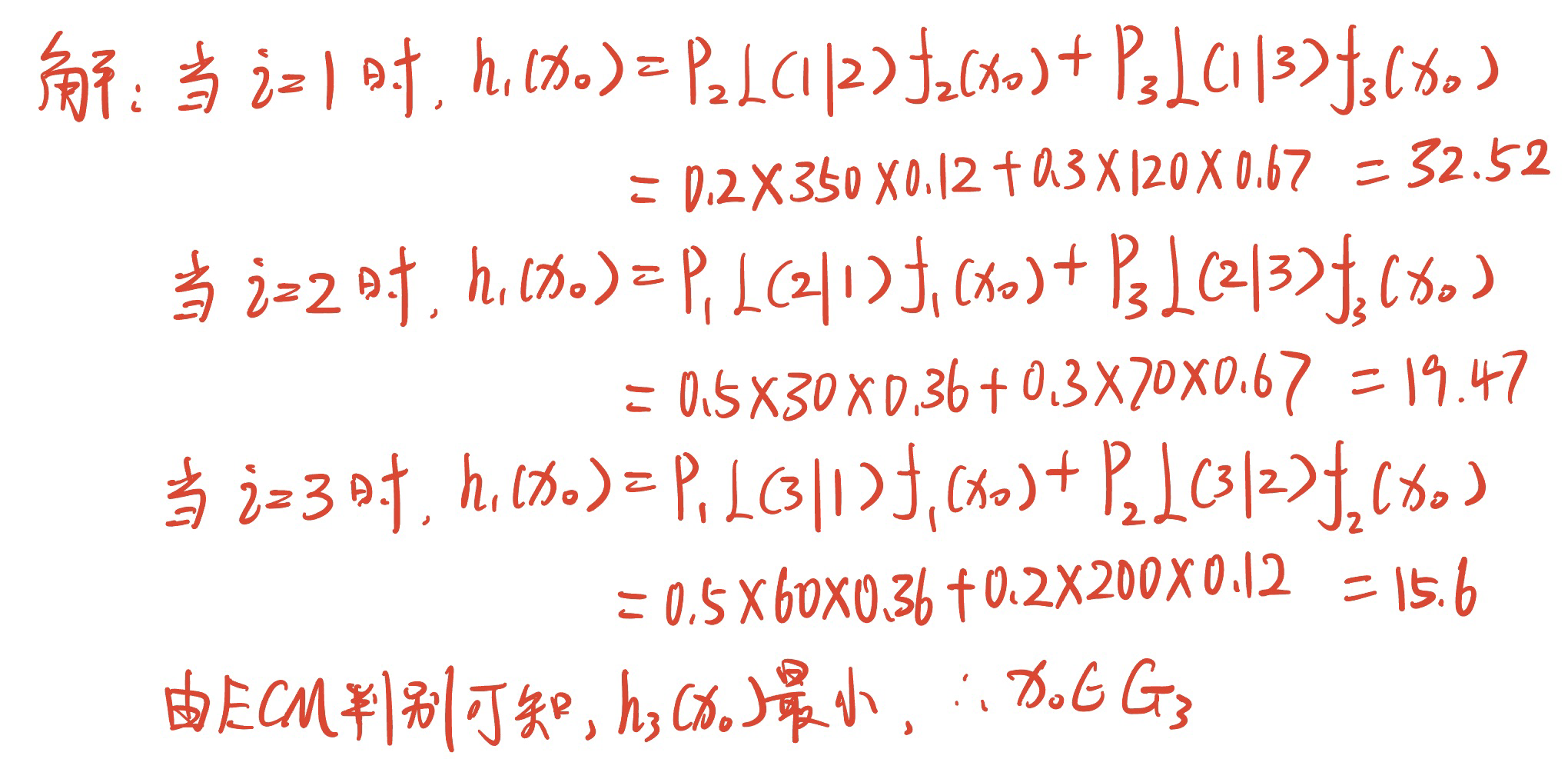
设有 5 个样本数据$1,2,5,7,10$。使用最长，最短距离法进行聚类分析，写出聚类步骤中各步距离矩阵，并画出谱系聚类图。
设三元总体$X$的协方差阵为$\Sigma = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 6 \end{bmatrix}$，从$\Sigma$出发，求总体主成分$Z_1,Z_2,Z_3$，并求前两个主成分的累积贡献率。

$u_3$应该是$\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}$
设三元总体$X$的协方差阵为$\Sigma = \begin{bmatrix} 1 & 2 \\ 2 &1 \end{bmatrix} $，从$\Sigma$出发，求第一主成分$Z_1$的贡献率。
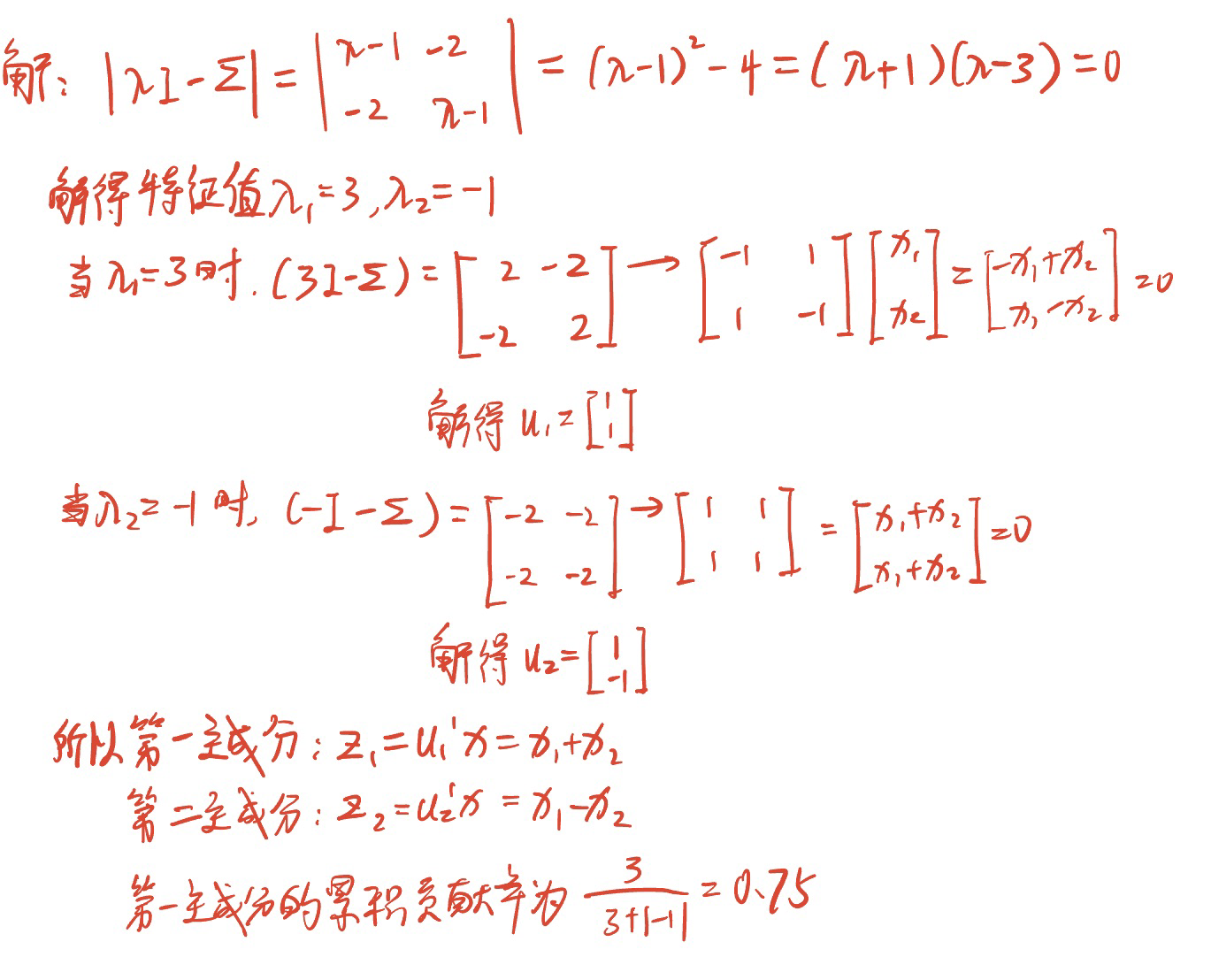
简述费希尔判别的基本思想。

费希尔（Fisher）判别的基本思想是投影，或降维。对于来自不同总体（类）的高维数据，选择若干个好的投影方向将它们投影为低维数据，使得这些来自不同类的低维数据之间有比较清晰的界限。对于新样品对应的高维数据点，也将其以同样方向投影为一个低维数据点，然后再利用一般的距离判别方法判断其属于哪一类。而衡量类与类之间是否分开的方法借助于一元方差分析的思想。
简述$k$均值聚类法的基本思想及该算法的具体步骤。

K 均值聚类法又称为逐步聚类法，其基本思想是，开始时先选择一批凝聚点或给出一个初始分类，让样品按照某种原则向凝聚点凝聚，并对凝聚点进行不断的更新或迭代，直至分类比较合理或迭代达到稳定为止，这样就形成一个最终的分类结果。

k 均值聚类算法的具体步骤如下：
1. 第一步，指定聚类数目 k。在 k 均值聚类过程中，要求首先给出聚类数目。
2. 第二步，确定 k 个初始中心凝聚点，或者将所有样品分成 k 个初始类，然后将这 k 个类的重心（均值）作为初始中心凝聚点。
3. 第三步，根据最近原则进行聚类。依次计算每个观测点到 k 个中心凝聚点的距离，并按照离中心凝聚点最近的原则，将所有样品分配到最近的类中，形成 k 个类。
4. 第四步，重新确定 k 个类的中心点。依次计算各类的重心，即各类中所有样品点的均值，并以重心点作为 k 个类的新的中心凝聚点。
5. 第五步，判断是否已经满足聚类算法的迭代终止条件，如果未满足则返回到第三步，并重复上述过程，直至满足迭代终止条件。
主成分分析的基本思想。

主成分分析就是一种通过降维技术把多个指标约化为少数几个综合指标的统计分析方法。其基本思想是：设法将原来众多具有一定相关性的指标，重新组合成一组新的相互无关的综合指标来代替原来指标。数学上的处理就是将原来 p 个指标的若干个线性组合作为新的指标。
因子分析的基本思想。

基本思想：把每个研究变量分解为几个影响因素变量，将每个原始变量分解成两部分因素，一部分是由所有变量共同具有的少数几个公共因子组成的，另一部分是每个变量独自具有的因素，即特殊因子。
系统聚类法的基本思想基本思想。

首先将每个样品视为单点类，即每个样品自成一类。然后逐次进行类的合并，每次将具有最小距离的两个类合并在一起，合并后重新计算类与类之间的距离，这个过程一直继续到所有的样品归为一类为止，并把这个过程画成一张系统聚类图。

为研究某地区的综合发展状况，研究人员收集了该地区 10 年的经济发展、社会状况等方面的统计数据，包括总人口数量($x_1$)，GDP($x_2$)，社会固定资产投资($x_3$)，城市化水平($x_4$)，人均居住面积($x_5$)，客运量($x_6$)，如图所示。

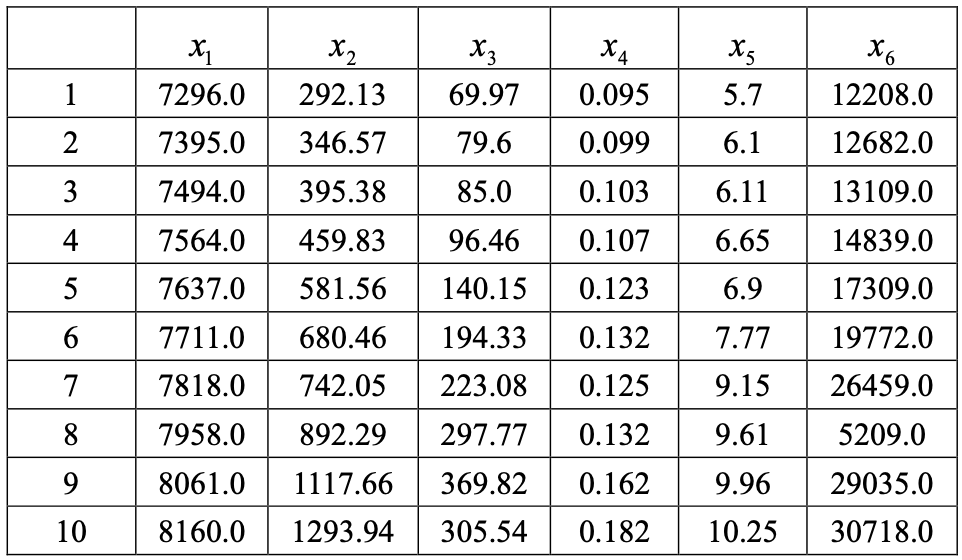
试对该数据资料使用主成分法、主因子法、极大似然法求因子载荷阵的估计值。（$累计贡献率 \ge 90 %$）

> EcoData <- read.csv("EcoData.csv",head=TRUE)
> EcoData <- EcoData[,-1]
> print(EcoData)
     X1      X2     X3    X4    X5    X6
1  7296  292.13  69.97 0.095  5.70 12208
2  7395  346.57  79.60 0.099  6.10 12682
3  7494  395.38  85.00 0.103  6.11 13109
4  7564  459.83  96.46 0.107  6.65 14839
5  7637  581.56 140.15 0.123  6.90 17309
6  7711  680.46 194.33 0.132  7.77 19772
7  7818  742.05 223.08 0.125  9.15 26459
8  7958  892.29 297.77 0.132  9.61 25209
9  8061 1117.66 369.82 0.162  9.96 29035
10 8160 1293.94 305.54 0.182 10.25 30718
> R <- cor(EcoData)
> library("psych")
> # 主成分法
> pc <- principal(r=R,nfactors=2,rotate="none");pc
Principal Components Analysis
Call: principal(r = R, nfactors = 2, rotate = "none")
Standardized loadings (pattern matrix) based upon correlation matrix
    PC1   PC2   h2     u2 com
X1 0.99  0.00 0.98 0.0171 1.0
X2 0.99  0.12 1.00 0.0022 1.0
X3 0.97 -0.14 0.97 0.0322 1.0
X4 0.96  0.29 1.00 0.0024 1.2
X5 0.98 -0.16 0.99 0.0052 1.1
X6 0.99 -0.10 0.98 0.0183 1.0

                       PC1  PC2
SS loadings           5.77 0.15
Proportion Var        0.96 0.03
Cumulative Var        0.96 0.99
Proportion Explained  0.97 0.03
Cumulative Proportion 0.97 1.00

Mean item complexity =  1.1
Test of the hypothesis that 2 components are sufficient.

The root mean square of the residuals (RMSR) is  0.01

Fit based upon off diagonal values = 1
> # 主因子法
> fa <- fa(r=R,nfactors=2,fm="pa",rotate="none");fa
Factor Analysis using method =  pa
Call: fa(r = R, nfactors = 2, rotate = "none", fm = "pa")
Standardized loadings (pattern matrix) based upon correlation matrix
    PA1   PA2   h2       u2 com
X1 0.99  0.00 0.98  0.02136 1.0
X2 0.99  0.11 1.00  0.00049 1.0
X3 0.97 -0.10 0.94  0.05797 1.0
X4 0.96  0.28 0.99  0.00761 1.2
X5 0.99 -0.18 1.00 -0.00439 1.1
X6 0.98 -0.10 0.98  0.02232 1.0

                       PA1  PA2
SS loadings           5.75 0.14
Proportion Var        0.96 0.02
Cumulative Var        0.96 0.98
Proportion Explained  0.98 0.02
Cumulative Proportion 0.98 1.00

Mean item complexity =  1.1
Test of the hypothesis that 2 factors are sufficient.

df null model =  15  with the objective function =  18.92
df of  the model are 4  and the objective function was  0.67

The root mean square of the residuals (RMSR) is  0
The df corrected root mean square of the residuals is  0

Fit based upon off diagonal values = 1
> # 极大似然法
> f1 <- factanal(EcoData,2,rot="none");f1
Call:
factanal(x = EcoData, factors = 2, rotation = "none")

Uniquenesses:
   X1    X2    X3    X4    X5    X6
0.019 0.005 0.055 0.005 0.005 0.016

Loadings:
   Factor1 Factor2
X1  0.989
X2  0.996
X3  0.960   0.155
X4  0.970  -0.234
X5  0.974   0.216
X6  0.979   0.160

               Factor1 Factor2
SS loadings      5.739   0.158
Proportion Var   0.957   0.026
Cumulative Var   0.957   0.983

Test of the hypothesis that 2 factors are sufficient.
The chi square statistic is 5.58 on 4 degrees of freedom.
The p-value is 0.233
>

写出三种方法下的因子模型。
- 主成分法：
  - $x_1 = 0.99f_1 $
  - $ x_2 = 0.99f_1 + 0.12f_2 $
  - $ x_3 = 0.97f_1 - 0.14f_2 $
  - $ x_4 = 0.96f_1 + 0.29f_2 $
  - $ x_5 = 0.98f_1 - 0.16f_2 $
  - $ x_6 = 0.99f_1 - 0.1f_2$
- 主因子法：
  - $x_1 = 0.99f_1 $
  - $ x_2 = 0.99f_1 + 0.11f_2 $
  - $ x_3 = 0.97f_1 - 0.1f_2 $
  - $ x_4 = 0.96f_1 + 0.28f_2 $
  - $ x_5 = 0.99f_1 - 0.18f_2 $
  - $ x_6 = 0.98f_1 - 0.1f_2$
- 极大似然法：
  - $x_1 = 0.989f_1 $
  - $ x_2 = 0.996f_1 $
  - $ x_3 = 0.96f_1 + 0.155f_2 $
  - $ x_4 = 0.97f_1 - 0.234f_2 $
  - $ x_5 = 0.974f_1 - 0.216f_2 $
  - $ x_6 = 0.979f_1 - 0.16f_2$

写出三种方法中的因子方差，方差贡献率及方差累计贡献率。

公因子	主成分法方差	方差贡献率	方差累计贡献率	主因子法方差	方差贡献率	方差累计贡献率	极大似然法方差	方差贡献率	方差累计贡献率
1	5.77	0.96	0.96	5.75	0.96	0.96	5.739	0.957	0.957
2	0.15	0.03	0.99	0.14	0.02	0.98	0.158	0.026	0.983

为了分析媒体网站的定位，对中国媒体网站进行评价。根据 Alexa 网站提供的评价指标，选取了 5 项指标作为媒体网站的评价标准，评价数据如图所示。

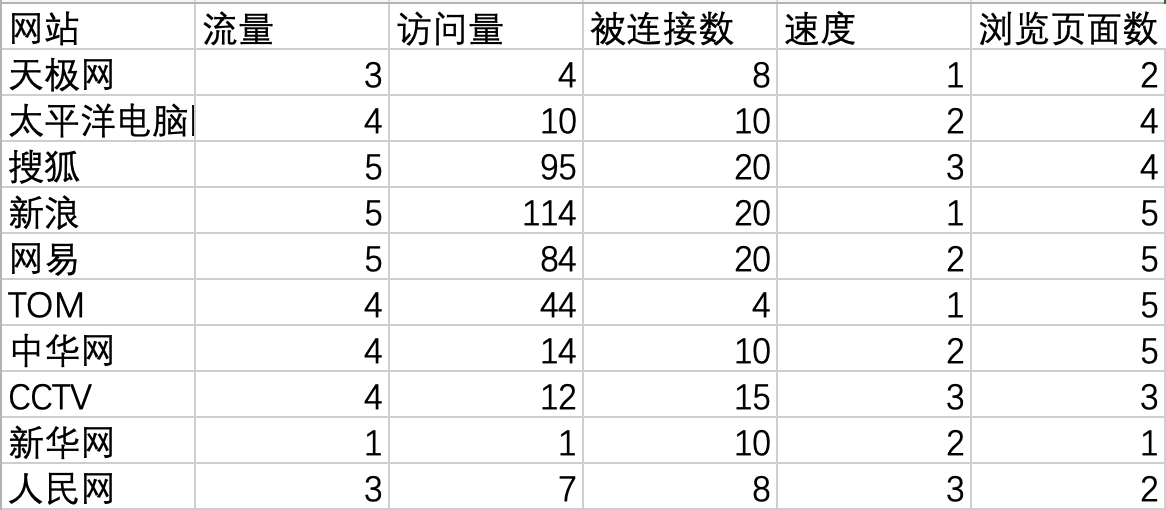
取$m = 2$，写出$Q$型与$R$型的因子载荷矩阵。

> data <- read.csv("Alexa.csv",head=TRUE)
> data <- data[,-1]
> library("MASS")
> ca1 <- corresp(data,2)
> ca1
First canonical correlation(s): 0.4333964 0.1433618

Row scores:
            [,1]       [,2]
[1,] -1.9322470  0.7437385
[2,] -1.4227035  1.4687414
[3,]  0.5117460 -0.5152798
[4,]  0.7261601 -0.3201458
[5,]  0.4219459 -0.3100543
[6,]  0.6266890  1.6841660
[7,] -1.0873964  1.7653308
[8,] -1.5429105 -0.5296207
[9,] -2.8878094 -3.5136091
[10,] -1.7240602  0.1395799

Column scores:
         [,1]        [,2]
x1 -1.1696327  2.01246755
x2  0.7417411 -0.07074029
x3 -1.3044761 -1.10746752
x4 -2.1685686 -0.62338275
x5 -0.9637053  2.82395385

试对该数据进行分析。

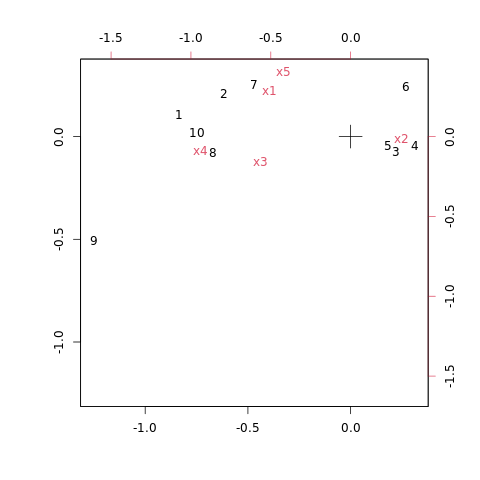
对某地区的某类消费品的销量$y$进行调查，它与下面 4 个变量相关:居民可收入支配$x_1$，该类消费品评价价格指数$x_2$，该产品的社会保有量$x_3$，其他消费品评价价格指数$x_4$，历史资料如图所示。试求

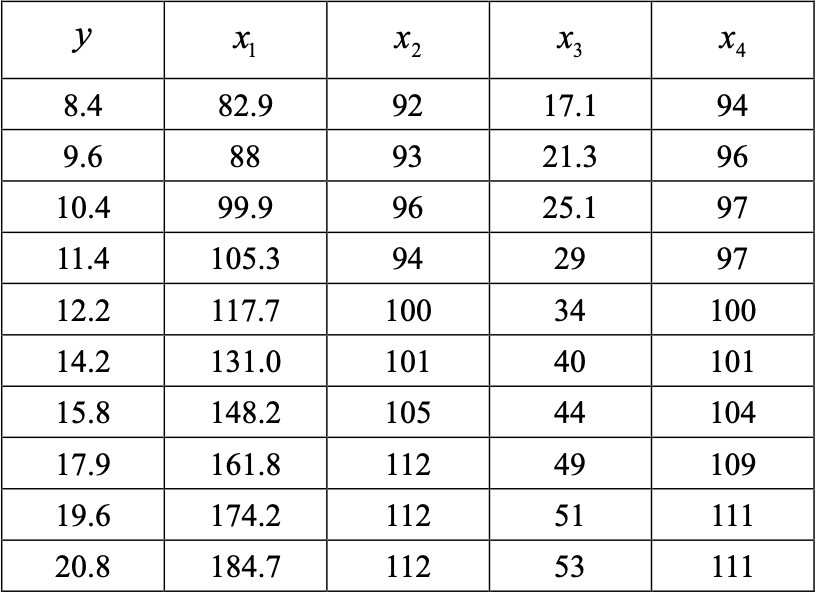
普通线性回归方程。

> data <- read.csv("biao001.csv",head=TRUE)
> lm.sol <- lm(y~x1+x2+x3+x4,data=data)
> summary(lm.sol)
Call:
lm(formula = y ~ x1 + x2 + x3 + x4, data = data)

Residuals:
        1         2         3         4         5         6         7         8
 0.024803  0.079476  0.012381 -0.007025 -0.288345  0.216090 -0.142085  0.158360
        9        10
-0.135964  0.082310

Coefficients:
             Estimate Std. Error t value Pr(>|t|)
(Intercept) -17.66768    5.94360  -2.973  0.03107 *
x1            0.09006    0.02095   4.298  0.00773 **
x2           -0.23132    0.07132  -3.243  0.02287 *
x3            0.01806    0.03907   0.462  0.66328
x4            0.42075    0.11847   3.552  0.01636 *
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.2037 on 5 degrees of freedom
Multiple R-squared:  0.9988,	Adjusted R-squared:  0.9978
F-statistic:  1021 on 4 and 5 DF,  p-value: 1.827e-07

$y = -17.66768 + 0.09006x_1 - 0.23132x_2 + 0.01806x_3 + 0.42075x_4$

利用主成分回归建立销售量$y$与 4 个变量的回归方程。（保留 4 位小数）

> conomy<-read.csv("biao001.csv",head=TRUE)
> conomy.pr<-princomp(~x1+x2+x3+x4,data=conomy,cor=T)
> pre <- predict(conomy.pr)
> conomy $ z1 <- pre[,1]
> conomy $ z2 <- pre[,2]
> lm.sol <- lm(y~z1+z2,data=conomy)
> summary(lm.sol)
Call:
lm(formula = y ~ z1 + z2, data = conomy)

Residuals:
   Min       1Q   Median       3Q      Max
-0.74323 -0.29223  0.01746  0.30807  0.80849

Coefficients:
            Estimate Std. Error t value Pr(>|t|)
(Intercept) 14.03000    0.17125  81.927 1.06e-11 ***
z1           2.06119    0.08623  23.903 5.70e-08 ***
z2           0.62409    0.85665   0.729     0.49
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.5415 on 7 degrees of freedom
Multiple R-squared:  0.9879,	Adjusted R-squared:  0.9845
F-statistic: 285.9 on 2 and 7 DF,  p-value: 1.945e-07
> beta <- coef(lm.sol)
> A <- loadings(conomy.pr)
> x.bar <- conomy.pr$center
> x.sd <- conomy.pr$scale
> coef <- (beta[2]*A[,1]+beta[3]*A[,2])/x.sd
> c(beta0,coef)
(Intercept)           x1           x2           x3           x4
-16.88460655   0.03420968   0.09376460   0.11954881   0.12360237

$y = -16.8846 + 0.0342x_1 + 0.0938x_2 + 0.1195x_3 + 0.1236x_4$

将$n = 1000$个人组成的样本按人的心理健康与其父母社会经济地位进行交叉分类，心理健康程度分为:0(心理健康)，1(轻微症状)，2(中度症状)，3(心理受损)共 4 个等级，父母经济地位按照高低分为$A, B, C, D, E$五个等级。分类结果见表。

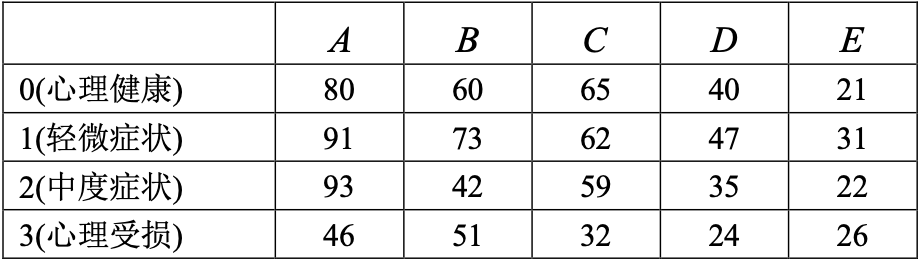
取$m = 2$，写出$Q$型与$R$型的因子载荷矩阵。

> data <- read.csv("biao002.csv", head=TRUE)
> data
index  A  B  C  D  E
1     0 80 60 65 40 21
2     1 91 73 62 47 31
3     2 93 42 59 35 22
4     3 46 51 32 24 26
> library("MASS")
> ca1 <- corresp(data, 2)
> ca1
First canonical correlation(s): 0.13611576 0.07820638

Row scores:
         [,1]       [,2]
[1,]  0.5596349  1.1053713
[2,] -0.1772184  0.5860922
[3,]  0.9968915 -1.4080092
[4,] -1.9067299 -0.6404426

Column scores:
            [,1]       [,2]
index -4.7797857 -8.8467932
A      0.7973588 -0.7688971
B     -1.1290698  0.9792588
C      0.7815115  0.2709922
D      0.1603097  0.6227149
E     -1.5710745 -0.7986631

试对该数据进行分析。

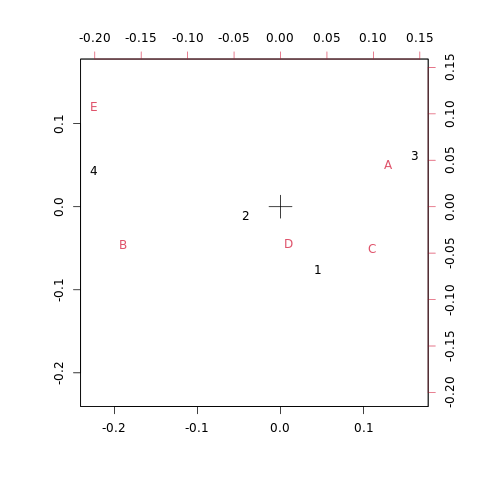
设标准化变量$x = (x_1, x_2, x_3)’$的相关矩阵$R = \begin{bmatrix} 1 & 0.48 & 0.76 \\ 0.48 & 1 & 0.23 \\ 0.76 & 0.23 & 1 \end{bmatrix}$，$R$的特征值和相应的单位正交特征向量为：
$\lambda_1 = 2.0131760 \quad u_1 = (0.6624437, 0.4498215, 0.5990243)’$
$\lambda_2 = 0.7950835 \quad u_2 = (0.1218358, -0.853693, 0.5063243)’$
$\lambda_3 = 0.1917404 \quad u_3 = (0.7391376, -0.2624289, -0.6203279)’$
1. 求$m = 1$时的因子模型的主成分解。
2. 求$m = 2$时的因子载荷矩阵$A$。
3. 计算共性方差$h_i^2$的值并解释其统计意义。
4. 求公因子$f_1, f_2$的方差贡献。
5. 计算相关系数$cov(x_i, f_1)(i = 1, 2, 3)$，并说明哪个变量在公因子$f_1$上有最大载荷。（保留 4 位小数）
1. $A = \sqrt{\lambda_1}u_1 = 1.4189u_1 = (0.9399, 0.6383, 0.8499)$
  因子模型：
  - $x_1 = 0.9399f_1 + \varepsilon_1$
  - $x_2 = 0.6383f_1 + \varepsilon_2$
  - $x_3 = 0.8499f_1 + \varepsilon_3$
2. $A = (\sqrt{\lambda_1}u_1, \sqrt{\lambda_2}u_2) = \begin{bmatrix} 0.9399 & 0.1086 \\ 0.6383 & -0.7612 \\ 0.8499 & 0.4515 \end{bmatrix}$
3. - $h_1^2 = 0.9399^2 + 0.1086^2 = 0.8952$
  - $h_2^2 = 0.6383^2 + (-0.7612)^2 = 0.9869$
  - $h_3^2 = 0.8499^2 + 0.4515^2 = 0.9262$
  - $h_1^2$表示公因子$f_1, f_2$对样本数据$x_1$的方差贡献为 0.8952
  - $h_2^2$表示公因子$f_1, f_2$对样本数据$x_2$的方差贡献为 0.9869
  - $h_3^2$表示公因子$f_1, f_2$对样本数据$x_3$的方差贡献为 0.4515
4. - $g_1^2 = 0.9399^2 + 0.6383^2 + 9.8499^2 = 2.0132$
  - $g_2^2 = 0.1086^2 + (-0.7612)^2 + 0.4515^2 = 0.7951$
  - $g_1^2$表示$f_1$对变量$x_1, x_2, x_3$的方差贡献为 2.0132
  - $g_2^2$表示$f_2$对变量$x_1, x_2, x_3$的方差贡献为 0.7951
5. $cov(x_1, f_1) = 0.9399 \quad cov(x_2, f_1) = 0.6838 \quad cov(x_3, f_1) = 0.8499$
  比较可知$cov(x_1, f_1) = 0.9399$最大，故变量$x_1$在公因子$f_1$上有最大载荷。
设标准化变量$x = (x_1, x_2, x_3)’$的相关矩阵$R = \begin{bmatrix} 1 & 0.56 & 0.3 \\ 0.56 & 1 & 0.35 \\ 0.3 & 0.35 & 1 \end{bmatrix}$，$R$的特征值和相应的单位正交特征向量为：
$\lambda_1 = 1.86 \quad u_1 = (0.53, 0.57, 0.61)’$
$\lambda_2 = 0.65 \quad u_2 = (-0.22, -0.49, 0.84)’$
$\lambda_3 = 0.39 \quad u_3 = (0.65, -0.64, -0.18)’$
1. 求$m = 1$时的因子模型的主成分解。
2. 求$m = 2$时的因子载荷矩阵$A$。
3. 计算共性方差$h_i^2$的值并解释其统计意义。
4. 求公因子$f_1, f_2$的方差贡献。
5. 计算相关系数$cov(x_i, f_1)(i = 1, 2, 3)$，并说明哪个变量在公因子$f_1$上有最大载荷。（保留 4 位小数）
1. $A = \sqrt{\lambda_1}u_1 = 1.3638u_1 = (0.7228, 0.7774, 0.8319)$
  因子模型：
  - $x_1 = 0.7228f_1 + \varepsilon_1$
  - $x_2 = 0.7774f_1 + \varepsilon_2$
  - $x_3 = 0.8319f_1 + \varepsilon_3$
2. $A = (\sqrt{\lambda_1}u_1, \sqrt{\lambda_2}u_2) = \begin{bmatrix} 0.7228 & -0.1774 \\ 0.7774 & -0.3950 \\ 0.8319 & 0.6772 \end{bmatrix}$
3. - $h_1^2 = 0.7228^2 + (-0.1774)^2 = 0.5539$
  - $h_2^2 = 0.7774^2 + (-0.3950)^2 = 0.7604$
  - $h_3^2 = 0.8319^2 + 0.6772^2 = 1.1507$
  - $h_1^2$表示公因子$f_1, f_2$对样本数据$x_1$的方差贡献为 0.5539
  - $h_2^2$表示公因子$f_1, f_2$对样本数据$x_2$的方差贡献为 0.7604
  - $h_3^2$表示公因子$f_1, f_2$对样本数据$x_3$的方差贡献为 1.1507
4. - $g_1^2 = 0.7228^2 + 0.7774^2 + 0.8319^2 = 1.8189$
  - $g_2^2 = (-0.1774)^2 + (-0.3950)^2 + 0.6712^2 = 0.6461$
  - $g_1^2$表示$f_1$对变量$x_1, x_2, x_3$的方差贡献为 1.8189
  - $g_2^2$表示$f_2$对变量$x_1, x_2, x_3$的方差贡献为 0.6461
5. $cov(x_1, f_1) = 0.7228 \quad cov(x_2, f_1) = 0.7774 \quad cov(x_3, f_1) = 0.8319$
  比较可知$cov(x_3, f_1) = 0.8319$最大，故变量$x_3$在公因子$f_1$上有最大载荷。

PDF

应用多元统计分析复习题.pdf

/citation/resources/应用统计学复习题/应用多元统计分析复习题.pdf

Orlando

填空题

判断题

计算题

PDF

你的赏识是我前进的动力